题目内容
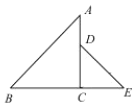
【题目】如图,![]() ,
,![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,且
,且![]() ,点
,点![]() 是
是![]() 的中点,延长
的中点,延长![]() 、
、![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
(1)求证:![]()
(2)若![]() ,
,![]() ,求
,求![]() 的周长和
的周长和![]() 的长.
的长.
【答案】(1)见解析;(2)△AMC的周长=![]() +5
+5![]() +8;
+8;![]() .
.
【解析】
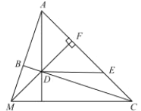
(1)如图,首先证明DF⊥AE,DF=AF=EF,这是解决问题的关键性结论;运用AAS证明△DFC≌△AFM;
(2)依次求出FM、FC、AC、AM、MC,即可![]() 的周长;利用面积公式
的周长;利用面积公式![]() ,即可求出
,即可求出![]() 的长.
的长.
(1)证明:∵![]() ,且
,且![]() ,
,
∴△ADE是等腰直角三角形,
∵F是AE中点,
∴DF⊥AE,DF=AF=EF;
又∵∠ABC=90°,∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF;
在△DFC与△AFM中,
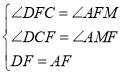 ,
,
∴△DFC≌△AFM(AAS).
(2)解:∵∠ADE=90°,AD=DE,AF=FE,
∴DF=EF=AF=3,
∵DM=2,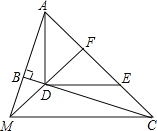
∴FM= 5,
∵△DFC≌△AFM,
∴FC= FM=5,
∴AC=8,
∵∠CFM=90°,
∴CM=5![]() ,AM=
,AM=![]() ,
,
∴△AMC的周长=![]() +5
+5![]() +8,
+8,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目