题目内容
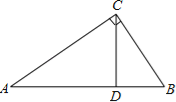
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、 点
、 点![]() 分别在线段
分别在线段![]() 和线段
和线段![]() 上,
上, ![]() 平分
平分![]() .
.
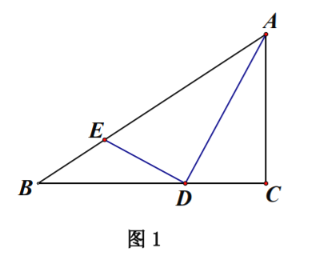
![]() 如图1,求证:
如图1,求证:![]() .
.
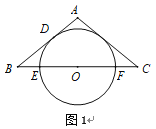
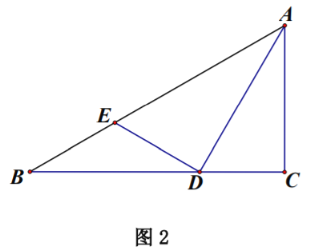
![]() 如图2,若
如图2,若![]() .求证:
.求证:![]() .
.
![]() 在
在![]() 问的条件下,如图3, 在线段
问的条件下,如图3, 在线段![]() 上取一点
上取一点![]() ,使
,使![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
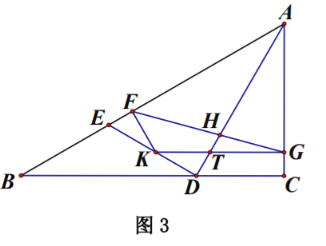
【答案】(1)见解析;(2)见解析;(3)DT=![]() -1
-1
【解析】
(1)先根据∠AED+∠ADB=180°,∠ADB+∠ADC=180°,得出∠AED=∠ADC,进而得到△ADE∽△ACD,即可得出∠ADE=∠C=90°;
(2)先设BE=x,则AE=2x,通过证明△ADB∽△DEB,列比例式可得BD的长,根据三角函数可得∠EAD=∠CAD=30°,可得结论;
(3)如图3,过E作ER⊥BC于R,延长ED、AC交于点M,过G作GN⊥EM于N,先根据AE=2BE,可得BE和ED的长,设FL=x,根据AF=AL+FL列方程可得x的值,表示KD、KN和GN的长,根据DT∥NG,得△KDT∽△KNG,列比例式可得DT的长.
证明:(1)如图1,∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠AED+∠ADB=180°,∠ADB+∠ADC=180°,
∴∠AED=∠ADC,
∴△ADE∽△ACD,
∴∠ADE=∠C=90°,
∴AD⊥DE;
(2)如图2,设BE=x,则AE=2x,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠AED+∠ADB=180°,
∠AED+∠BED=180°,
∴∠ADB=∠BED,
∵∠B=∠B,
∴△ADB∽△DEB,
∴![]() ,
,
∴![]() ,
,
∴BD2=3x2,
∴BD=![]() x,
x,
∴![]() ,
,
∴∠AED=60°,
∴∠EAD=∠CAD=30°,
∴∠B=30°,
∴AB=2AC;
(3)如图3,过E作ER⊥BC于R,延长ED、AC交于点M,过G作GN⊥EM于N,
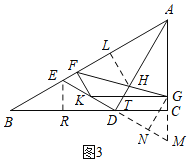
∵AE=2![]() +2,AE=2BE,
+2,AE=2BE,
∴BE=![]() +1,
+1,
∵∠ADC=60°,∠ADE=90°,
∴∠EDB=∠B=30°,
∴BE=DE=![]() +1,
+1,
∴BD=2BR,
Rt△BER中,ER=![]() BE=
BE=![]() BR=
BR=![]() ,
,
∴BD=2BR=3+![]() =AD=AF,
=AD=AF,
Rt△ADC中,∠DAC=30°,
∴DC=![]() AD=
AD=![]() ,CM=
,CM=![]() ,
,
DM=![]() +1,
+1,
Rt△EFK中,EF=AE-AF=2![]() +2-(
+2-(![]() +3)=
+3)=![]() -1,
-1,
∵∠AEK=60°,
∴EK=2EF=2![]() -2,
-2,
∴DK=![]() +1-(2
+1-(2![]() -2)=3-
-2)=3-![]() ,
,
∵∠AFH=45°,∠FAH=30°=∠GAH,
∴∠AHG=75°,∠AGH=180°-30°-75°=75°,
∴AG=AH,
过H作HL⊥AF于L,
∵∠LFH=45°,
∴FL=HL,
设FL=x,则HL=x,AH=AG=2x,AL=![]() x,
x,
∵AL+FL=AF,
∴x+![]() x=3+
x=3+![]() ,
,
x=![]() ,
,
∴AG=2![]() ,
,
∴CG=AC-AG=![]() AB-AG=
AB-AG=![]() (2
(2![]() +2+
+2+![]() +1)-2
+1)-2![]() ,
,
∴GM=CG+CM=2,
R△GNM中,∠M=60°,∠NGM=30°,
∴MN=![]() GM=1,
GM=1,
∴DN=DM-MN=![]() +1-1=
+1-1=![]() ,GN=
,GN=![]() ,
,
∴KN=KD+DN=3-![]() +
+![]() =3,
=3,
∵DT//NG,
∴△KDT∽△KNG,
∴![]() ,
,
∴![]() ,
,
∴DT=![]() -1.
-1.

 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点M为顶点,连接OM,若y与x的部分对应值如表所示:
x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点M为顶点,连接OM,若y与x的部分对应值如表所示:
x | … | ﹣1 | 0 | 3 | … |
y | … | 0 |
| 0 | … |
(1)求抛物线的解析式;
(2)抛物线与y轴交于点C,点Q是直线BC下方抛物线上一点,点Q的横坐标为xQ.若S△BCQ≥![]() S△BOC,求xQ的取值范围;
S△BOC,求xQ的取值范围;
(3)如图2,平移此抛物线使其顶点为坐标原点,P(0,﹣1)为y轴上一点,E为抛物线上y轴左侧的一个动点,从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F.则当E点位置变化时,直线EF是否经过某个定点?如果是,请求出此定点的坐标;若不是,请说明理由.