题目内容
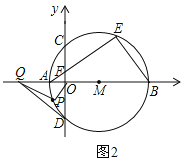
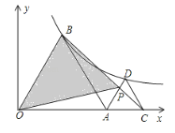
【题目】如图，△AOB和△ACD均为正三角形，且顶点B、D均在双曲线
（x＞0）上，若图中S△OBP＝4，则k的值为（ ）
A.
B.－C.－4D.4
【答案】D
【解析】
先根据△AOB和△ACD均为正三角形可知∠AOB=∠CAD=60°，故可得出AD∥OB，所以S△OBP=S△AOB，过点B作BE⊥OA于点E，由反比例函数系数k的几何意义即可得出结论．
解：∵△AOB和△ACD均为正三角形，
∴∠AOB=∠CAD=60°，
∴AD∥OB，
∴S△OBP=S△AOB，
∵S△OBP＝4
∴S△AOB＝4
过点B作BE⊥OA于点E，
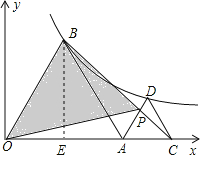
则S△OBE=S△ABE=
S△AOB，
∴S△OBE=×4=2，
∵点B、D均在双曲线
（x＞0）上，由反比例函数系数k的几何意义,
∴k的值为4．
故选D．
练习册系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c（a≠0）中的x和y满足下表：
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | －1 | 0 | m | 8 | … |
（1）可求得m的值为________；
（2）在坐标系画出该函数的图象；
（3）当y≥0时，x的取值范围为_____________
