Question

【题目】在正方形中，，对角线交于点,点在线段上，且,将射线绕点逆时针转，交于点, 则的长为____________．

Answer 1

【答案】或

【解析】

根据正方形的性质得到AC=6，AC⊥BD，求得AO=BO=，CP=4，根据勾股定理得到PB=，根据相似三角形的性质即可得到结论．

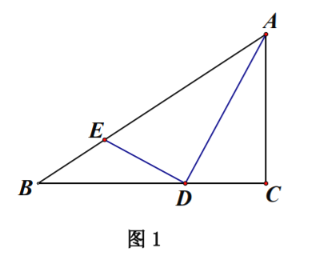
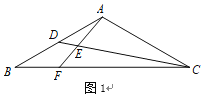
解：如图1，

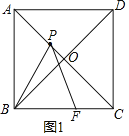
在正方形ABCD中，AB=6，

∴AC=6，AC⊥BD，
∴AO=BO=AC=3，

∵OP=，

∴CP=4，

在Rt△BPO中，PB=，

∵∠BPF=∠BAP=∠PCF=45°，

∴∠APB=∠PFC=135°-∠FPC，

∴△APB∽△CFP，

∴，即，

∴PF=，

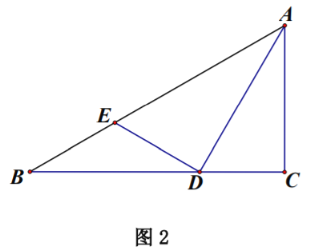
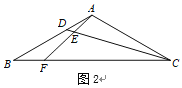
如图2，

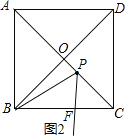
在正方形ABCD中，AB=6，

∴AC=6，AC⊥BD，

∴AO=BO=AC=3，

∵OP=，

∴CP=2，

在Rt△BPO中，PB=，

∵∠BPF=∠BAP=∠PCF=45°，

∴∠APB=∠PFC=135°-∠FPC，

∴△APB∽△CFP，

∴，即，

∴PF=，

综上所述：PF的长为或，

故答案为：或．