Question

【题目】对于平面中给定的一个图形及一点 P，若图形上存在两个点 A、B，使得△PAB 是边长为 2 的等边三角形，则称点 P 是该图形的一个“美好点”．

（1）若将 x 轴记作直线 l，下列函数的图象上存在直线 l 的“美好点”的是 （只填选项）

A．正比例函数 y x

B．反比例函数 y

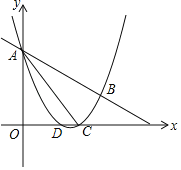
C．二次函数 y x 2

（2）在平面直角坐标系 xOy 中，若点 M (n, 0) ， N (0, n) ，其中n0 ，⊙O 的半径为 r．

①若r 2，⊙O 上恰好存在 2 个直线 MN 的“美好点”，求 n 的取值范围；

②若n4 ，线段 MN 上存在⊙O 的“美好点”，直接写出 r 的取值范围．

Answer 1

【答案】（1）A，B　　（2）①2＜＜6，②．

【解析】

（1）把每个函数的图像画好，利用美好点的定义画出符合条件的等边直接可以作出判断．

（2）①弄懂题意，将直线MN沿轴平移，利用空间想象能力找到一个美好点时，三个美好点时的模型，然后利用不等式组求得的范围．

②沿①问的思路直接列出不等式求解．

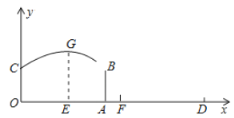
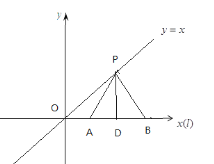
解：（1）如下图：P是直线的美好点，则是边长为2的等边三角形，所以，过P作 垂足为D，则又P是直线上的点，所以，所以，所以，所以上存在的美好点．故A正确．

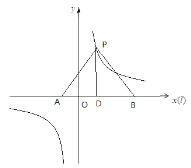
如下图：P是直线的美好点，则是边长为2的等边三角形，所以，过P作 垂足为D，则又P是直线上的点，所以P的纵坐标是，把纵坐标代入函数解析式的横坐标为 所以，所以上存在的美好点．故B正确．

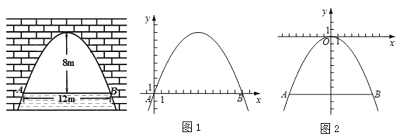
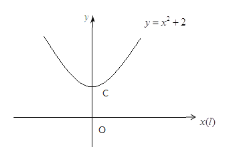
如下图，抛物线的顶点C（0，2），所以上的点与上的点之间最短距离是2，所以上不存在的美好点．

故答案为A，B．

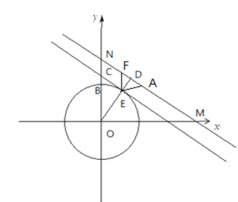
（2）①如图，当直线MN与⊙O相离时，因为M (n, 0) ， N (0, n)（）所以直线MN的解析式为：，，

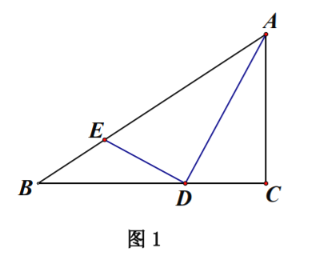
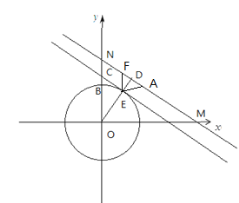
将直线NN平移到与⊙O相切，切点为E，与轴交于点C，连接OE，延长OE与MN交于点D，则，当E为MN的美好点时，此时⊙O 上存在一个MN的美好点，此时ED＝，所以当⊙O上恰好存在MN的两个美好点，则，

又由 所以，所以，

所以，解得： ．

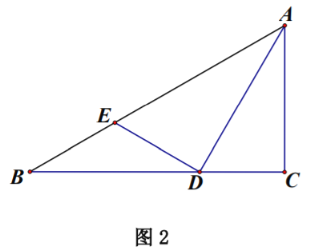
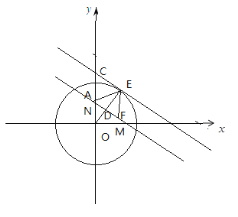
当直线MN与⊙O相交时，如下图，同理当时，由对称性知道⊙O上存在MN的三个美好点，然后会出现四个美好点，所以此时，此时，所以，解得：．综上的取值范围为： ．

②如下图，当n4，则M (, 0) ， N (0, 4)，此时，将直线NN平移到与⊙O相切，切点为E，与轴交于点C，连接OE，延长OE与MN交于点D，则，当E为MN的美好点时，此时⊙O 上存在一个MN的美好点，此时ED＝，若线段 MN 上存在⊙O 的“美好点”，则 ，

所以，解得：