题目内容
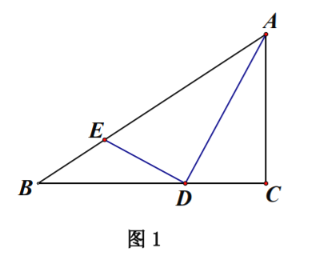
【题目】如图，在Rt△ABC中，∠ACB=90°，CD是边AB上的高．
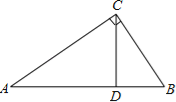
（1）求证：△ABC∽△CBD；
（2）如果AC=4，BC=3，求BD的长．
【答案】（1）证明见解析，（2）
【解析】试题分析：（1）根据相似三角形的判定，由已知可证∠A=∠DCB，又因为∠ACB=∠BDC=90°，即证△ABC∽△CBD，
（2）根据勾股定理得到AB=5，根据三角形的面积公式得到CD=
，然后根据勾股定理即可得到结论．
（1）证明：∵CD⊥AB，
∴∠BDC=90°．
∴∠A+∠ACD=90°．
∵∠ACB=90°，
∴∠DCB+∠ACD=90°．
∴∠A=∠DCB．
又∵∠ACB=∠BDC=90°，
∴△ABC∽△CBD；
（2）解：∵∠ACB=90°，AC=4，BC=3，
∴AB=5，
∴CD=，
∵CD⊥AB，
∴BD=
=
=
．
练习册系列答案
相关题目
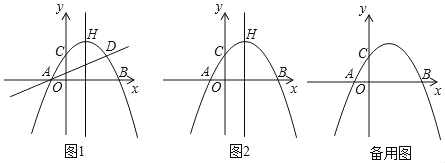
【题目】已知二次函数y=ax2+bx+c（a≠0）中的x和y满足下表：
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | －1 | 0 | m | 8 | … |
（1）可求得m的值为________；
（2）在坐标系画出该函数的图象；
（3）当y≥0时，x的取值范围为_____________
