题目内容
【题目】在平面直角坐标系中，抛物线y＝﹣
x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点M为顶点，连接OM，若y与x的部分对应值如表所示：
x | … | ﹣1 | 0 | 3 | … |
y | … | 0 |
| 0 | … |
（1）求抛物线的解析式；
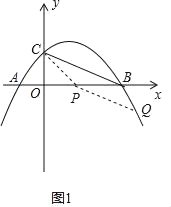
（2）抛物线与y轴交于点C，点Q是直线BC下方抛物线上一点，点Q的横坐标为xQ．若S△BCQ≥S△BOC，求xQ的取值范围；
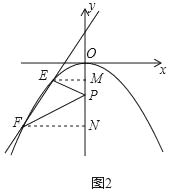
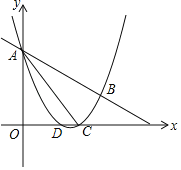
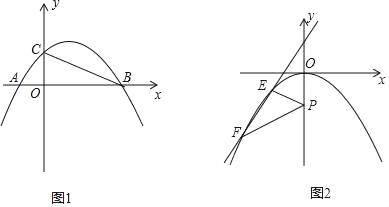
（3）如图2，平移此抛物线使其顶点为坐标原点，P（0，﹣1）为y轴上一点，E为抛物线上y轴左侧的一个动点，从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F．则当E点位置变化时，直线EF是否经过某个定点？如果是，请求出此定点的坐标；若不是，请说明理由．
【答案】（1）y＝﹣
x2+x+
；（2）xQ≥
或xQ≤
；（3）定点（0，1）．
【解析】
（1）由抛物线y＝﹣x2+bx+c与x轴交于A、B两点，（﹣1，0），（3，0），即可求得抛物线的解析式；
（2）首先取OB的中点P（，0），连接CP，然后过点P作PQ∥BC交抛物线于Q，首先求得直线BC的解析式，然后由平行线的性质，求得直线PQ的解析式，再联立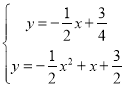
，即可求得答案；
（3）首先得到平移后的抛物线的解析式为：y＝﹣x2，再过点E作EM⊥y轴于M，过点F作FN⊥y轴于N，易得Rt△EPM∽Rt△FPN，再联立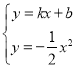
，即可求得答案．
解：（1）∵抛物线y＝﹣x2+bx+c与x轴交于A、B两点，（﹣1，0），（3，0），
∴y＝﹣（x+1）（x﹣3），
∴抛物线的解析式为：y＝﹣x2+x+；
（2）取OB的中点P（，0），连接CP，
则S△PBC＝S△BOC，
过点P作PQ∥BC交抛物线于Q，即为所求；
∵抛物线与y轴交于点C，
∴点C的坐标为：（0，），
设直线BC的解析式为y＝kx+b，
，
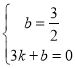解得：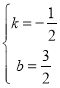
，
∴直线BC的解析式为y＝﹣x+，
∴设直线PQ的解析式为y＝﹣x+n，
∴﹣×+n＝0，
∴n＝
，
∴直线PQ的解析式为y＝﹣x+，
联立，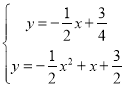
解得：x＝
，
若S△BCQ≥S△BOC
则xQ的取值范围为：xQ≥或xQ≤；
（3）平移后的抛物线的解析式为：y＝﹣x2，
过点E作EM⊥y轴于M，过点F作FN⊥y轴于N，
由反射可知：∠EPM＝∠FPN，
∴Rt△EPM∽Rt△FPN，
∴
，
设E（x1，y1）、F（x2，y2），设直线EF的解析式为y＝kx+b，
∴
，
∴x1（1+y2）+x2（y1+1）＝0，
联立，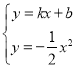
整理得x2+2kx+2b＝0，
∴x1+x2＝﹣2k，x1x2＝2b，
∵x1（1+y2）+x2（y1+1）＝x1（1+kx2+b）+x2（kx1+b+1）＝0，
∴2bx1x2+（b+1）（x1+x2）＝0，
∴2kb﹣2k＝0，b＝1，
∴直线EF的解析式为y＝kx+1
∴直线EF过定点（0，1）．
