题目内容
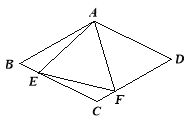
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )

A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
证明△BCO是等腰三角形即可证明①正确;由EG=![]() AB,EF=
AB,EF=![]() AB可证②成立;由中点的性质可得出EF∥CD,且EF=
AB可证②成立;由中点的性质可得出EF∥CD,且EF=![]() CD=BG,结合平行即可证得③结论成立;由三线合一可证明④成立;无法证明⑤成立;此题得解.
CD=BG,结合平行即可证得③结论成立;由三线合一可证明④成立;无法证明⑤成立;此题得解.
∵四边形ABCD是平行四边形,
∴BD=2BO,AD=BC,
∵BD=2AD,
∴BD=2BC,
∴BO=BC,
∵E为OC中点,
∴BE⊥AC,故①成立;
∵BE⊥AC,G是AB中点,
∴EG=![]() AB,
AB,
∵E、F分别是OC、OD的中点,
∴EF∥CD,且EF=![]() CD,
CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,且AB=CD,
∴EF=![]() AB,
AB,
∴EF=EG,故②成立;
∵AB∥CD,EF∥CD,
∴EF∥AB,
∴∠FEG=∠BGE(两直线平行,内错角相等),
在△EFG和△GBE中,
∵BG=FE,∠FEG=∠BGE,GE=EG,
∴△EFG≌△GBE(SAS),即③成立;
∵BG=FE,EF∥AB,
∴四边形BEFG是平行四边形,
∵BE⊥AC,
∴GF⊥AC,
∵EF=EG,
∴∠AEG=∠AEF,
即EA平分∠GEF
故④正确,
若四边形BEFG是菱形
∴BE=BG=![]() AB,
AB,
∴∠BAC=30°
与题意不符合
故⑤错误
故选C.

练习册系列答案
相关题目