题目内容
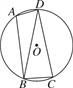
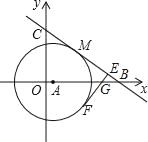
【题目】如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=﹣![]() x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
(1)直接写出b的值和点B的坐标;
(2)求点A的坐标和圆的半径;
(3)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求![]() 的值.
的值.
【答案】(1)y=﹣![]() x+7;B(
x+7;B(![]() ,0)(2)圆A的半径为5(3)3
,0)(2)圆A的半径为5(3)3
【解析】试题分析:(1)将点M的坐标代入直线![]() 的解析式可求得b的值,由b的值可得到直线的解析式,然后令y=0可求得点B的横坐标,于是得到点B的坐标;
的解析式可求得b的值,由b的值可得到直线的解析式,然后令y=0可求得点B的横坐标,于是得到点B的坐标;
(2)由相互垂直的两条直线的一次项系数为-1,可设直线AM的解析式为![]()
然后将点M的坐标代入可求得c的值,然后令y=0可求得点A的横坐标,最后依据两点间的距离公式可求得圆A的半径.
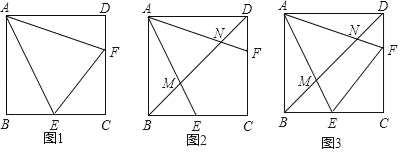
(3)如图1所示:连接AF、AM.先证明四边形AFEM为正方形,于是可求得ME=5,然后在△ABM中依据勾股定理可求得MB的长,从而可求得BE的长,接下来,证明![]() 由相似三角形的性质可求得答案.
由相似三角形的性质可求得答案.
试题解析:
(1)∵点M在直线![]() 上,
上,
![]() 解得:b=7.
解得:b=7.
∴直线的解析式为![]()
∵当y=0时, ![]() ,解得:
,解得: ![]()
![]()
(2)∵BC是圆A的切线,
∴AM⊥BC.
设直线AM的解析式为![]()
∵将M(4,4)代入![]() 得
得![]() 解得:
解得: ![]()
∴直线AM的解析式为![]()
∵当y=0时, ![]() 解得x=1,
解得x=1,
∴A(1,0).
∵由两点间的距离公式可知![]()
∴圆A的半径为5.
(3)如图1所示:连接AF、AM.
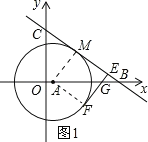
∵BC、EF是圆A的切线,
∴AM⊥BC,AF⊥EF.
又∵BC⊥EF,
![]()
∴四边形AFEM为矩形,
又∵AM=AF,
∴四边形AFEM为正方形,
∴ME=AF=5.
∵在Rt△AMB中, ![]()
![]()
![]()
∴△AGF∽△BGE.
![]() 即
即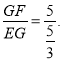
![]()

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目