题目内容
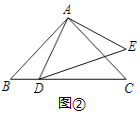
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
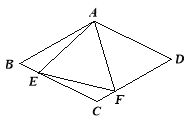
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
【答案】(1)证明过程见解析;(2)4+2![]()
【解析】
试题分析:(1)连接AC,根据菱形的性质以及∠BAD=120°得出∠BAE=∠FAC以及△ABC和△ACD为正三角形,从而得出△ABE和△ACF全等,从而得出答案;(2)根据三角形全等得出△ABE的面积=△ACF的面积,从而得出四边形AECF的面积=△ABC的面积,从而求出△ABC的面积得出四边形的面积,根据垂线段最短得出当正三角形AEF的边AE与BC垂直时,边AE最短,从而求出最小值.
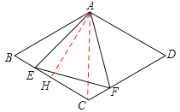
试题解析:(1)如图,连接AC∵四边形ABCD为菱形,∠BAD=120°,
∠BAE+∠EAC=60°,∠FAC+∠EAC=60°,∴∠BAE=∠FAC
∵∠BAD=120°,∴∠ABC=60°.∴△ABC和△ACD为等边三角形
∴∠ACF=60°,AC=AB ∴∠ABE=∠AFC ∴在△ABE和△ACF中,∵∠BAE=∠FAC,AB=AC,∠ABE=∠AFC,∴△ABE≌△ACF(ASA) ∴BE=CF
(2)四边形AECF的面积不变,△CEF的周长发生变化.理由如下:
由(1)得△ABE≌△ACF,则![]() .∴
.∴![]() ,是定值
,是定值
作AH⊥BC于H点,则BH=2,
![]() .
.
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE
由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小=4+![]() ,
,


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案