题目内容
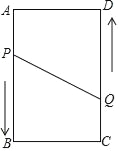
【题目】如图，A、B、C、D为矩形的四个顶点，AB=16cm，AD=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达B为止，点Q以2cm/s的速度向D移动．
(1)P、Q两点从出发开始到几秒时，四边形APQD为长方形？
(2)P、Q两点从出发开始到几秒时？四边形PBCQ的面积为33cm2；
(3)P、Q两点从出发开始到几秒时？点P和点Q的距离是10cm．
【答案】(1) P，Q两点从出发开始到3.2秒时，四边形APQD为长方形； (2) P，Q两点从出发开始到5秒时，四边形PBCQ的面积为33cm2；(3) P，Q两点从出发开始到1.6秒或4.8秒时，点P和点Q的距离是10cm．
【解析】
（1）当PB=CQ时，四边形PBCQ为矩形，依此建立方程求出即可；
（2）设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2，则PB=（16-3x）cm，QC=2xcm，根据梯形的面积公式可列方程：
，解方程可得解；
（3）作QE⊥AB，垂足为E，设运动时间为x秒，用x表示线段长，用勾股定理列方程求解．
(1)设P，Q两点从出发开始到x秒时，四边形APQD为长方形，
根据题意得：16﹣3x=2x，
解得：x=
．
答：P，Q两点从出发开始到秒时，四边形APQD为长方形．
(2)设P，Q两点从出发开始到y秒时，四边形PBCQ的面积为33cm2，
根据题意得：
×6（16﹣3x+2x）=33，
解得：x=5．
答：P，Q两点从出发开始到5秒时，四边形PBCQ的面积为33cm2．
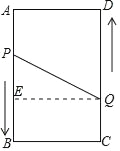
(3)过点Q作QE⊥AB于点E，如图所示．
设P，Q两点从出发开始到x秒时，点P和点Q的距离是10cm，
根据题意得：（16﹣3x﹣2x）2+62=102，
整理得：（16﹣5x）2=82，
解得：x1=
，x2=
．
答：P，Q两点从出发开始到秒或秒时，点P和点Q的距离是10cm．
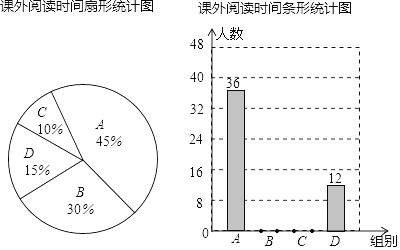
阅读快车系列答案
【题目】为了创建书香校园，切实引导学生多读书，读好书．某中学开展了“好书伴我成长”的读书节活动，为了了解本校学生每周课外阅读时间，随机抽取部分学生进行问卷调查，将课外阅读时间分为A、B、C、D四组，并利用臭氧所得的数据绘制了如下统计图．
组别 | 课外阅读t（单位：时） |
A | X＜2 |
B | 2≤x＜3 |
C | 3≤x＜4 |
D | x≥4 |
请根据图中提供的信息，解答下列问题：
（1）一共调查了________名学生；
（2）扇形统计图中A组的圆心角度数________；
（3）直接补全条形统计图
（4）若该校有2400名学生，根据你所调查的结果，估计每周课外阅读时间不足3小时的学生有多少人？
