题目内容
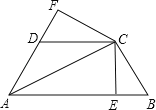
【题目】如图,河边有 A,B 两个村庄,A 村距河边 10m,B 村距河边 30m,两村平行于河边方 向的水平距离为 30m,现要在河边建一抽水站 E,需铺设管道抽水到 A 村和 B 村.

(1)要使铺设管道的长度最短,请作图找出水站 E 的位置(不写作法)
(2)若铺设管道每米需要 500 元,则最低费用为多少?
【答案】(1)见解析(2)25000元
【解析】
(1)先求出点A关于河流的对称点A′,然后连接A′B,与河流的交点E即为所求作的抽水站的位置.利用勾股定理求出A′B即为铺设管道的最短距离.
(2)运用费用=米数×每米的钱数.
(1)如图所示,抽水站修在点E处才能使所需的管道最短.

先求出点A关于河流的对称点A′,然后连接A′B,与河流的交点E即为所求作的抽水站的位置.
作BC垂直于河,A′C平行河.
∵两村的水平距离为30米,
∴A′C=30米.
∵A村距河边10米,B村距河边30米,
∴BC=10+30=40(米).
∴A′B=![]() =50(米).
=50(米).
(2)最低费用为:50×500=25000(元).

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目