题目内容
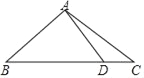
【题目】如图,已知△ABC中,AB=AC,∠C=30°,AB⊥AD.
(1)求∠BDA的度数;
(2)若AD=2,求BC的长.
【答案】(1)60°;(2)6.
【解析】
(1)由题意可得∠B=∠C=30°,由AB⊥AD,可求∠BDA的度数;
(2)根据30度所对的直角边等于斜边的一半,可求BD=4,根据三角形的外角等于不相邻的两个内角和,可求∠C=∠DAC=30°,可得AD=CD=2,即可求BC的长.
解:(1)∵AB=AC,
∴∠B=∠C=30°,
∵AD⊥AB,
∴∠BDA+∠B=90°,
∴∠BDA=60°;
(2)∵∠BDA=60°,∠C=30°,且∠BDA=∠C+∠DAC,
∴∠DAC=60°﹣30°=30°=∠C,
∴AD=CD=2,
∵AB⊥AD,∠B=30°,
∴BD=2AD=4,
∵BC=BD+CD,
∴BC=2+4=6.

练习册系列答案
相关题目