题目内容
在Rt△ABC中,∠C=90°,AC=1,BC= ,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):
,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):
以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),并回答下列问题:
∠ABC= ,∠A′BC= ,OA+OB+OC= .

 ,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):
,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),并回答下列问题:
∠ABC= ,∠A′BC= ,OA+OB+OC= .

解:作图如下:
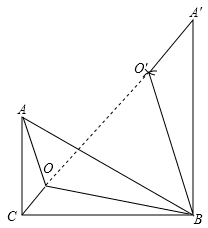
30°;90°; 。
。

30°;90°;
 。
。试题分析:按题意作图。
∵∠C=90°,AC=1,BC=
 ,∴
,∴ 。∴∠ABC=30°。
。∴∠ABC=30°。∵△AOB绕点B顺时针方向旋转60°,∴∠A′BC=∠ABC+60°=30°+60°=90°。
∵∠C=90°,AC=1,∠ABC=30°,∴AB=2AC=2。
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO。∴△BOO′是等边三角形。
∴BO=OO′,∠BOO′=∠BO′O=60°。
∵∠AOC=∠COB=BOA=120°,∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°。
∴C、O、A′、O′四点共线。
在Rt△A′BC中,
 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 (0°<
(0°<
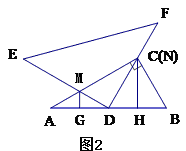

 的位置,若AE=1,BE=2,CE=3,则∠
的位置,若AE=1,BE=2,CE=3,则∠ = 度.
= 度.
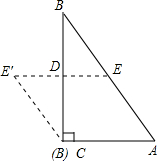


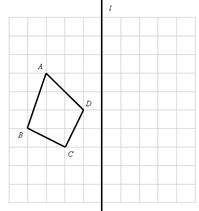
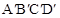 ,使四边形
,使四边形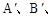
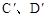 分别是点A、B、C、D的对称点;
分别是点A、B、C、D的对称点; 的长度。
的长度。
