题目内容
正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF.

(1)如图1,若点G是边BC的中点,连接FG,则EF与FG关系为: ;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转900,得到线段FQ,连接EQ,请猜想EF、EQ、BP三者之间的数量关系,并证明你的结论;
(3)若点P为CB延长线上一动点,按照(2)中的作法,在图3中补全图形,并直接写出EF、EQ、BP三者之间的数量关系: .

(1)如图1,若点G是边BC的中点,连接FG,则EF与FG关系为: ;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转900,得到线段FQ,连接EQ,请猜想EF、EQ、BP三者之间的数量关系,并证明你的结论;
(3)若点P为CB延长线上一动点,按照(2)中的作法,在图3中补全图形,并直接写出EF、EQ、BP三者之间的数量关系: .
解:(1)垂直且相等。
(2)EF、EQ、BP三者之间的数量关系为: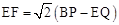 。
。
证明如下:
如图,取BC的中点G,连接FG,
由(1)得EF=FG,EF⊥FG,
根据旋转的性质,FP=FQ,∠PFQ =90°。
∴∠GFP=∠GFE—∠EFP=90°—∠EFP,
∠EFQ=∠PFQ—∠EFP=90°—∠EFP。
∴∠GFP=∠EFQ。
在△FQE和△FPG中,∵EF=GF,∠EFQ=∠GFP,FQ = FP,
∴△FQE≌△FPG(SAS)。∴EQ=GP。
∴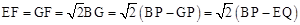 。
。
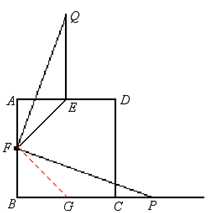
(3)补图如下,F、EQ、BP三者之间的数量关系为: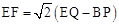 。
。
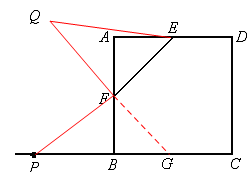
(2)EF、EQ、BP三者之间的数量关系为:
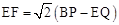 。
。证明如下:
如图,取BC的中点G,连接FG,

由(1)得EF=FG,EF⊥FG,
根据旋转的性质,FP=FQ,∠PFQ =90°。
∴∠GFP=∠GFE—∠EFP=90°—∠EFP,
∠EFQ=∠PFQ—∠EFP=90°—∠EFP。
∴∠GFP=∠EFQ。
在△FQE和△FPG中,∵EF=GF,∠EFQ=∠GFP,FQ = FP,
∴△FQE≌△FPG(SAS)。∴EQ=GP。
∴
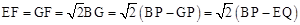 。
。(3)补图如下,F、EQ、BP三者之间的数量关系为:
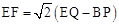 。
。
试题分析:(1)EF与FG关系为垂直且相等(EF=FG且EF⊥FG)。证明如下:
∵点E、F、G分别是正方形边AD、AB、BC的中点,
∴△AEF和△BGD是两个全等的等腰直角三角形。
∴EF=FG,∠AFE=∠BFG=45°。∴∠EFG=90°,即EF⊥FG。
(2)取BC的中点G,连接FG,则由SAS易证△FQE≌△FPG,从而EQ=GP,因此
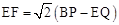 。
。(3)同(2)可证△FQE≌△FPG(SAS),得EQ=GP,因此,
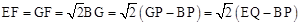 。
。
练习册系列答案
相关题目
 沿
沿 折叠,点
折叠,点 、
、 分别落在点
分别落在点 、
、 的位置,若
的位置,若 =110°,则∠1=______.
=110°,则∠1=______.
 ,为了使白球反弹后能将黑球直接撞入袋中,那么几大白球时,必须保证
,为了使白球反弹后能将黑球直接撞入袋中,那么几大白球时,必须保证 的度数为【 】
的度数为【 】




 ,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):
,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):
 的位置,其中
的位置,其中 交直线AD于点E,
交直线AD于点E,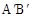 分别交直线AD、AC于点F、G,则在图(2)中,全等三角形共有
分别交直线AD、AC于点F、G,则在图(2)中,全等三角形共有





