题目内容
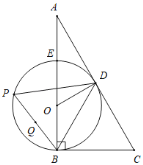
【题目】如图，
是⊙
的直径，点D是弧AC的中点，∠COD＝60°.
⑴三角形AOD是等边三角形吗？请说明理由；
⑵求证：OD∥BC .
【答案】（1）是，理由见解析（2）证明见解析.
【解析】
（1）根据弧、圆心角、弦之间的关系定理得到∠AOD=∠COD＝60°，即可得到三角形AOD是等边三角形；
（2）证明△COB为等边三角形，得到∠AOD=∠OBC＝60°，即可求解.
三角形AOD是等边三角形，证明如下：
∵点D是弧AC的中点，
∴∠AOD=∠COD＝60°
∵AO=DO,
∴三角形AOD是等边三角形；
（2）∵
是⊙
的直径，∠AOD=∠COD＝60°
∴∠COB＝180°-∠AOD-∠COD= 60°
又OC=OB，
△COB为等边三角形，
∴∠AOD=∠OBC＝60°，
故OD∥BC .
练习册系列答案
相关题目
【题目】水库90天内的日捕捞量y（kg）与时间第x（天）满足一次函数的关系，部分数据如表：
时间第x（天） | 1 | 3 | 6 | 10 |
日捕捞量（kg） | 198 | 194 | 188 | 180 |
（1）求出y与x之间的函数解析式；
（2）水库前50天采用每天降低水位的办法减少捕捞成本，到达最低水位标准后，后40天水库维持最低水位进行捕捞．捕捞成本和时间的关系如下表：
时间第x（天） | 1≤x＜50 | 50≤x≤90 |
捕捞成本（元/kg） | 60-x | 10 |
已知鲜鱼销售单价为每千克70元，假定该养殖场每天捕捞和销售的鲜鱼没有损失，且能在当天全部售出．设销售该鲜鱼的当天收入w元（当天收入=日销售额-日捕捞成本），
①请写出w与x之间的函数解析式，并求出90天内哪天收入最大？当天收入是多少？
②若当天收入不低于4800元，请直接写出x的取值范围？
