题目内容
【题目】水库90天内的日捕捞量y(kg)与时间第x(天)满足一次函数的关系,部分数据如表:
时间第x(天) | 1 | 3 | 6 | 10 |
日捕捞量(kg) | 198 | 194 | 188 | 180 |
(1)求出y与x之间的函数解析式;
(2)水库前50天采用每天降低水位的办法减少捕捞成本,到达最低水位标准后,后40天水库维持最低水位进行捕捞.捕捞成本和时间的关系如下表:
时间第x(天) | 1≤x<50 | 50≤x≤90 |
捕捞成本(元/kg) | 60-x | 10 |
已知鲜鱼销售单价为每千克70元,假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出.设销售该鲜鱼的当天收入w元(当天收入=日销售额-日捕捞成本),
①请写出w与x之间的函数解析式,并求出90天内哪天收入最大?当天收入是多少?
②若当天收入不低于4800元,请直接写出x的取值范围?
【答案】(1)y=-2x+200;(2)①第45天当天收入最大,最大收入为6050元;②当20≤x≤60时,当天收入不低于4800元
【解析】
(1)根据表格内数据,利用待定系数法即可求出y与x之间的函数解析式;
(2)①根据当天收入=日销售额-日捕捞成本即可找出w与x之间的函数解析式,再利用配方法及一次函数的性质,即可解决最值问题;
②分别求出w=-2x2+180x+2000(1≤x<50)中≥4800的x的取值范围及w=-120x+12000(50≤x≤70)中≥4800的x的取值范围,合在一起即可得出结论.
解:(1)设y与x之间的函数解析式为y=kx+b(k≠0),
将(1,198)、(3,194)代入y=kx+b中,
![]() ,解得:
,解得:![]() ,
,
∴y与x之间的函数解析式为y=-2x+200.
(2)①当1≤x<50时,w=70(-2x+200)-(-2x+200)(60-x)=-2x2+180x+2000;
当50≤x≤90时,w=70(-2x+200)-10(-2x+200)=-120x+12000.
∴w与x之间的函数解析式为w=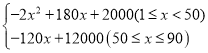 .
.
∵w=-2x2+180x+2000=-2(x-45)2+6050,
∴当x=45时,w=-2x2+180x+2000(1≤x<50)取最大值,最大值为6050;
∵w=-120x+12000中-120<0,
∴当x=50时,w=-120x+12000(50≤x≤90)取最大值,最大值为6000.
∵6050>6000,
∴第45天当天收入最大,最大收入为6050元.
②令-2x2+180x+2000≥4800,
解得:20≤x≤70,
∵20≤x<50,
∴20≤x<50;
令-120x+12000≥4800,
解得:x≤60,
∵50≤x≤70,
∴50≤x≤60.
综上所述:当20≤x≤60时,当天收入不低于4800元.