Question

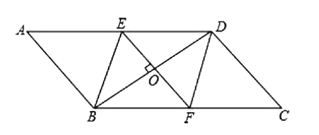
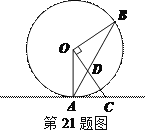
【题目】如图，Rt△ABC中，∠ABC＝90°，∠A＝30°，AC的垂直平分线交AC边于点D，交AB边于点O，以点O为圆心，OB的长为半径作圆，与AB边交于点E．

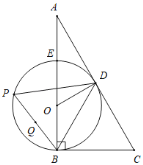
（1）求证：AC是⊙O的切线；

（2）若点P为⊙O上的动点（含点E，B），连接BD、BP、DP．

①当点P只在BE左侧半圆上时，如果BC∥DP，求∠BDP的度数；

②若Q是BP的中点，当BE＝4时，直接写出CQ长度的最小值．

Answer 1

【答案】（1）见解析；（2）①60°，②

【解析】

（1）连接OC，证明△ODC≌△OBC,说明OD＝OB，即可完成证明.

（2）①根据平行线的性质即可解答

②如图2中，连接OP，取OB的中点J，连接JQ,求出JQ，JC，根据CQ≥JC-JQ即可解决问题.

（1）证明：如图1中，连接OC．

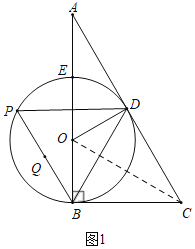
∵∠ABC＝90°，∠A＝30°，

∴∠ACB＝60°，

∵OD垂直平分线段AC，

∴OA＝OC，

∴∠A＝∠OCA＝30°，

∴∠OCB＝∠OCD＝30°，

∵∠ODC＝∠OBC＝90°，OC＝OC，

∴△ODC≌△OBC（AAS），

∴OD＝OB，

∴AC是⊙O的切线．

（2）①解：如图1中，∵DP∥BC，

∴∠PDB＝∠DBC，

∵∠ABC＝90°，AD＝DC，

∴BD＝DC＝AD，

∵∠DCB＝60°，

∴△BDC是等边三角形，

∴∠DBC＝60°，

∴∠BDP＝60°．

②解：如图2中，连接OP，取OB的中点J，连接JQ．

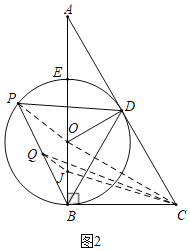
∵BE＝4，

∴OB＝OE＝OD＝OP＝2，JO＝JB＝1，

∵∠OBC＝90°，∠OCB＝30°，

∴BC＝OB＝2，

∴JC＝＝＝，

∵QP＝QB，JO＝JB，

∴JQ＝OP＝1，

∵CQ≥JC﹣JQ，

∴CQ≥﹣1，

∴CQ的最小值为﹣1．