题目内容
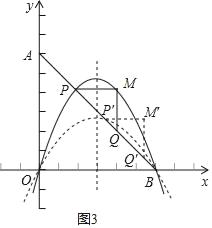
【题目】在平面直角坐标系中，点A是y轴上一点，其坐标为（0，6），点B在x轴的正半轴上．点P，Q均在线段AB上，点P的横坐标为m，点Q的横坐标大于m，在△PQM中，若PM∥x轴，QM∥y轴，则称△PQM为点P，Q的“肩三角形．
（1）若点B坐标为（4，0），且m＝2，则点P，B的“肩三角形”的面积为 ；
（2）当点P，Q的“肩三角形”是等腰三角形时，求点B的坐标；
（3）在（2）的条件下，作过O，P，B三点的抛物线y＝ax2+bx+c
①若M点必为抛物线上一点，求点P，Q的“肩三角形”面积S与m之间的函数关系式，并写出自变量m的取值范围．
②当点P，Q的“肩三角形”面积为3，且抛物线y＝ax2+bx+c与点P，Q的“肩三角形”恰有两个交点时，直接写出m的取值范围．
【答案】（1）3；（2）（6，0）；（3）①S＝2m2﹣12m+18（0＜m＜3）；②m＝3﹣
或3≤m≤6﹣
．
【解析】
（1）先利用待定系数法求出直线AB解析式，进而可得点P、M坐标，然后根据三角形的面积公式求解即可；
（2）根据题意可得MP＝MQ，∠PMQ＝90°，进而可得OB与OA的关系，问题即得解决；
（3）①因为M点必为抛物线上一点，所以可先确定自变量m取值范围，然后利用待定系数法求出直线AB的表达式，由抛物线y＝ax2+bx+c经过O，B两点，根据抛物线的对称性可确定抛物线的对称轴，设出点P的坐标后即得点Q的坐标，进而可求得PM的长，进一步即可求出S与m之间的函数关系式；
②当点P在对称轴左侧，利用①中的关系式即可求出m的值；当点P在对称轴上或对称轴右侧时，由“肩三角形”面积为3可求出PQ的长，于是可用m的代数式表示出Q、M的坐标，进一步即得关于m的不等式组，解不等式组即得结果.
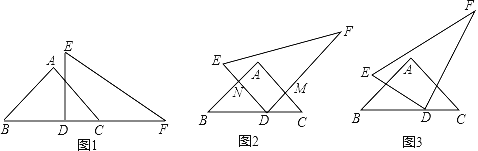
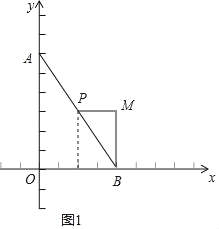
解：（1）如图1，∵A（0，6），B（4，0），
∴直线AB解析式为y＝﹣
x+6，
∵m＝2，∴P（2，3），
∵PM∥x轴，BM∥y轴，
∴M（4，3），∠PMB＝90°，
∴PM＝2，BM＝3，
∴点P，B的“肩三角形”△PBM的面积＝
PMBM＝×2×3＝3；
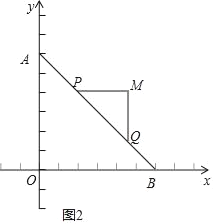
（2）如图2，根据题意，得MP＝MQ，∠PMQ＝90°，
∴∠MPQ＝45°，
∴∠ABO＝45°，
∴OB＝OA＝6，
∴点B的坐标为（6，0）；
（3）如图3，①因为M点必为抛物线上一点，所以自变量m取值范围为：0＜m＜3，
由（2）易得，直线AB的表达式为y＝6﹣x，
∴点P的坐标为（m，6﹣m），
∵抛物线y＝ax2+bx+c经过O，B两点，
∴抛物线的对称轴为直线x＝3，
∴点M的坐标为（6﹣m，6﹣m），
∴PM＝（6﹣m）﹣m＝6﹣2m，
S＝PM2＝×（6﹣2m）2＝2m2﹣12m+18（0＜m＜3）；
②当点P在对称轴左侧，即0＜＜3时，∵点P，Q的“肩三角形”面积为3，
由①得：2m2﹣12m+18＝3，解得：m＝3﹣（已舍去不合题意的）；
当点P在对称轴上或对称轴右侧，即3≤m＜6时，由点P，Q的“肩三角形”面积为3可得PM＝，
∴M（m+，6﹣m），Q（m+，6﹣﹣m）
∵抛物线＝ax2+bx+c与点P，Q的“肩三角形”恰有两个交点，
∴
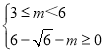，解得：3≤m≤6﹣，
综上所述，m的取值范围为：m＝3﹣或3≤m≤6﹣．
