题目内容
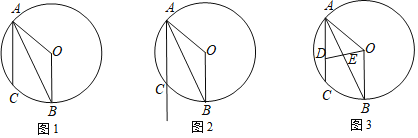
【题目】在圆O中,AO、BO是圆O的半径,点C在劣弧![]() 上,
上,![]() ,
,![]() ,
,![]() ,联结AB.
,联结AB.
![]() 如图1,求证:AB平分
如图1,求证:AB平分![]() ;
;
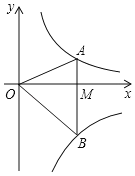
![]() 点M在弦AC的延长线上,联结BM,如果
点M在弦AC的延长线上,联结BM,如果![]() 是直角三角形,请你在如图2中画出点M的位置并求CM的长;
是直角三角形,请你在如图2中画出点M的位置并求CM的长;
![]() 如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D与点C的距离为x,
如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D与点C的距离为x,![]() 的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.
的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.
【答案】(1)见解析 (2)为4或8 (3)![]()
【解析】分析:(1)由![]() 知
知![]() ,根据
,根据![]() 知
知![]() ,据此可得
,据此可得![]() ,即可得证;(2)
,即可得证;(2)![]() 时,作
时,作![]() 可得
可得![]() ,由勾股定理求得
,由勾股定理求得![]() ,根据矩形OBMH知
,根据矩形OBMH知![]() ,由
,由![]() 可得答案;
可得答案;![]() 时,由
时,由![]() 可知
可知![]() 、
、![]() ,在
,在![]() 中根据
中根据![]() 可得
可得![]() ,继而得出答案;(3)作
,继而得出答案;(3)作![]() ,由
,由![]() 知
知![]() ,从而
,从而![]() ,结合
,结合![]() 求得
求得![]() ,根据
,根据![]() 知
知![]() ,即
,即![]() ,据此求得
,据此求得![]() ,利用
,利用![]() 可得答案.
可得答案.
详解:![]() 、OB是
、OB是![]() 的半径,
的半径,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 平分
平分![]() ;
;
![]() 由题意知,
由题意知,![]() 不是直角,
不是直角,
所以![]() 是直角三角形只有以下两种情况:
是直角三角形只有以下两种情况:![]() 和
和![]() ,
,
![]() 当
当![]() ,点M的位置如图1,
,点M的位置如图1,
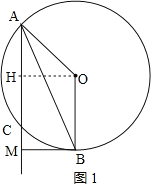
过点O作![]() ,垂足为点H,
,垂足为点H,
![]() 经过圆心,
经过圆心,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形OBMH是矩形,
四边形OBMH是矩形,
![]() 、
、![]() ,
,
![]() ;
;
![]() 当
当![]() ,点M的位置如图2,
,点M的位置如图2,
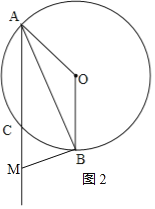
由![]() 可知,
可知,![]() 、
、![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
则![]() ,
,
综上所述,CM的长为4或8;
![]() 如图3,过点O作
如图3,过点O作![]() 于点G,
于点G,

由![]() 知
知![]() ,
,
由![]() 可得
可得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() 、
、![]() 、
、![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

【题目】某市在城中村改造中,需要种植![]() 、
、![]() 两种不同的树苗共
两种不同的树苗共![]() 棵,经招标,承包商以
棵,经招标,承包商以![]() 万元的报价中标承包了这项工程,根据调查及相关资料表明,
万元的报价中标承包了这项工程,根据调查及相关资料表明, ![]() 、
、![]() 两种树苗的成本价及成活率如表:
两种树苗的成本价及成活率如表:
品种 | 购买价(元/棵) | 成活率 |
|
|
|
|
|
|
设种植![]() 种树苗
种树苗![]() 棵,承包商获得的利润为
棵,承包商获得的利润为![]() 元.
元.
(![]() )求
)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(![]() )政府要求栽植这批树苗的成活率不低于
)政府要求栽植这批树苗的成活率不低于![]()
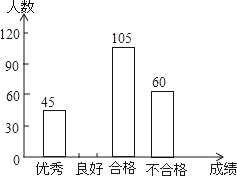
【题目】为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
成绩 | 频数 | 频率 |
优秀 | 45 | b |
良好 | a | 0.3 |
合格 | 105 | 0.35 |
不合格 | 60 | c |
(1)该校初三学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.