题目内容
【题目】如图,在△ABC中,AD、CE是△ABC的高,AF=BC,BE=3,AE=5.
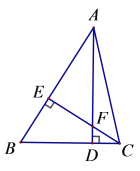
(1)图中有全等的三角形吗?请找出来并加以证明;
(2)求线段CF的长.
【答案】(1)△ BCE≌△FAE;见解析;(2)CF= 2.
【解析】
(1)要证明△AEF≌△CEB,由题意可得,AF=BC,由AD和CE是△ABC的高,可得∠AEF=∠CEB,然后再证明∠EAF=∠ECB即可;
(2)由(1)知,BE=EF,AE=EC,然后求得CF的长度.
(1)△ BCE≌ △FAE
证明:∵AD、CE是△ABC的高,
∴∠AEC=∠BEC=∠ADB=90°,
∴∠BCE+∠B=90°, ∠BAD+∠B=90°
∴∠BCE=∠BAD
在△BCE和△FAE中
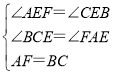
∴△BCE≌△FAE(AAS),
(2)由(1)得: CE= AE=5 ,EF=EB=3.
∴ CF= CE- EF=2

练习册系列答案
相关题目