题目内容
如图,抛物线y=x2-2mx+n+1的顶点A在x轴负半轴上,与y轴交于点B,C是抛物线上一点,且 点C的横坐标为1,AC=3
点C的横坐标为1,AC=3
.
(1)求抛物线的函数关系式;
(2)若D是抛物线上一点,直线BD经过第一、二、四象限,且原点O到直线BD的距离为
,求点D的坐标;
(3)在(2)的条件下,直线BD上是否存在点P,使得以A、B、P为顶点的三角形与△AOB相似?若存在,求出点P的坐标;若不存在,请说明理由.
 点C的横坐标为1,AC=3
点C的横坐标为1,AC=3| 10 |
(1)求抛物线的函数关系式;
(2)若D是抛物线上一点,直线BD经过第一、二、四象限,且原点O到直线BD的距离为
8
| ||
| 5 |
(3)在(2)的条件下,直线BD上是否存在点P,使得以A、B、P为顶点的三角形与△AOB相似?若存在,求出点P的坐标;若不存在,请说明理由.
(1)过点C作CE⊥x轴于点E,如图,
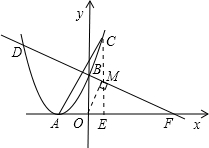 ∵抛物线上一点C的横坐标为1,
∵抛物线上一点C的横坐标为1,
∴C(1,n-2m+2),
其中n-2m+2>0,OE=1,CE=n-2m+2;
∵抛物线的顶点A在x轴负半轴上,
∴A(m,0),△=4m2-4(n+1)=0,得n=m2-1①,
其中m<0,OA=-m,AE=OE+OA=1-m,
在Rt△ACE中,AC=3
,
∵AE2+CE2=AC2,
∴(1-m)2+(n-2m+2)2=(3
)2②,
把①代入②得[(m-1)2]2+(m-1)2-90=0,
∴[(m-1)2+10][(m-1)2-9]=0,
∴(m-1)2-9=0
∴m1=4,m2=-2,
∵m<0,
∴m=-2.
把m=-2代入①,得n=4-1=3,
∴抛物线的关系式为y=x2+4x+4;
(2)设直线DB交x轴正半轴于点F,过点O作OM⊥DB于点M,如图,
∵点O到直线DB的距离为
,
∴OM=
,
而B点坐标为(0,4),
∴OB=4,
∴BM=
=
;
∵OB⊥OF,OM⊥BF,
∴△OBM∽△FOM,
∴
=
,即
=
,
∴OF=8,
∴F点坐标为(8,0),
设直线DB的解析式为y=kx+b,
把F(8,0)、B(0,4)代入得
,解得
,
∴直线DB的解析式为y=-
x+4,
解方程组
得
或
,
∴D点坐标为(-
,
);
(3)存在.理由如下:
∵OB=4,OF=8,
∴BF=
=4
,
∵y=(x+2)2,
∴A点坐标为(-2,0),
∴OA=2,
而OB=4,
∴AB=
=2
∴OA:OB=OB:OF,
∴△OAB∽△OBF,
∴∠AOB=∠OFB,
∴∠ABF=∠ABO+∠OBF=∠OFB+∠OBF=90°,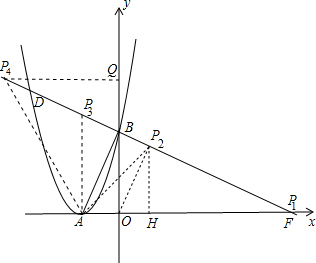
∴△ABF∽△AOB,
此时P1在F点位置,符号要求,P1点的坐标为(8,0);
当△ABP2∽△BOA时,
则BP2:OA=AB:BO,即BP2:2=2
:4,
∴BP2=
,
过P2作P2H⊥x轴于H,如图,
∴OH:OF=BP2:BF,即OH:8=
:4
,
∴OH=2,
把x=2代入y=-
x+4得y=-
×2+4=2,
∴P2的坐标为(2,2);
当△ABP3∽△BOA时,同样得到BP3=
,
∴P3A⊥OA,
∴P3的横坐标为-2,
把x=-2代入y=-
x+4得y=-
×(-2)+4=5,
∴P3的坐标为(-2,6);
当△ABP4∽△AOB时,
则BP4:OB=AB:AO,即BP4:4=2
:2,
∴BP4=4
,
过P4作P4Q⊥y轴于Q,如图,
易证得△P4QB≌△FOB,
∴P4Q=8,
把x=-8代入y=-
x+4得y=-
×(-8)+4=8,
∴P4的坐标为(-8,8),
∴满足条件的P点坐标为(-8,8)、(-2,5)、(2,2)、(8,0).
 ∵抛物线上一点C的横坐标为1,
∵抛物线上一点C的横坐标为1,∴C(1,n-2m+2),
其中n-2m+2>0,OE=1,CE=n-2m+2;
∵抛物线的顶点A在x轴负半轴上,
∴A(m,0),△=4m2-4(n+1)=0,得n=m2-1①,
其中m<0,OA=-m,AE=OE+OA=1-m,
在Rt△ACE中,AC=3
| 10 |
∵AE2+CE2=AC2,
∴(1-m)2+(n-2m+2)2=(3
| 10 |
把①代入②得[(m-1)2]2+(m-1)2-90=0,
∴[(m-1)2+10][(m-1)2-9]=0,
∴(m-1)2-9=0
∴m1=4,m2=-2,
∵m<0,
∴m=-2.
把m=-2代入①,得n=4-1=3,
∴抛物线的关系式为y=x2+4x+4;
(2)设直线DB交x轴正半轴于点F,过点O作OM⊥DB于点M,如图,
∵点O到直线DB的距离为
8
| ||
| 5 |
∴OM=
8
| ||
| 5 |
而B点坐标为(0,4),
∴OB=4,
∴BM=
| OB2-OM2 |
4
| ||
| 5 |
∵OB⊥OF,OM⊥BF,
∴△OBM∽△FOM,
∴
| OM |
| BM |
| OF |
| BO |
| OF |
| 4 |
| ||||
|
∴OF=8,
∴F点坐标为(8,0),
设直线DB的解析式为y=kx+b,
把F(8,0)、B(0,4)代入得
|
|
∴直线DB的解析式为y=-
| 1 |
| 2 |
解方程组
|
|
|
∴D点坐标为(-
| 9 |
| 2 |
| 25 |
| 4 |
(3)存在.理由如下:
∵OB=4,OF=8,
∴BF=
| OB2+OF2 |
| 5 |
∵y=(x+2)2,
∴A点坐标为(-2,0),
∴OA=2,
而OB=4,
∴AB=
| OB2+OA2 |
| 5 |
∴OA:OB=OB:OF,
∴△OAB∽△OBF,
∴∠AOB=∠OFB,
∴∠ABF=∠ABO+∠OBF=∠OFB+∠OBF=90°,

∴△ABF∽△AOB,
此时P1在F点位置,符号要求,P1点的坐标为(8,0);
当△ABP2∽△BOA时,
则BP2:OA=AB:BO,即BP2:2=2
| 5 |
∴BP2=
| 5 |
过P2作P2H⊥x轴于H,如图,
∴OH:OF=BP2:BF,即OH:8=
| 5 |
| 5 |
∴OH=2,
把x=2代入y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴P2的坐标为(2,2);
当△ABP3∽△BOA时,同样得到BP3=
| 5 |
∴P3A⊥OA,
∴P3的横坐标为-2,
把x=-2代入y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴P3的坐标为(-2,6);
当△ABP4∽△AOB时,
则BP4:OB=AB:AO,即BP4:4=2
| 5 |
∴BP4=4
| 5 |
过P4作P4Q⊥y轴于Q,如图,
易证得△P4QB≌△FOB,
∴P4Q=8,
把x=-8代入y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴P4的坐标为(-8,8),
∴满足条件的P点坐标为(-8,8)、(-2,5)、(2,2)、(8,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
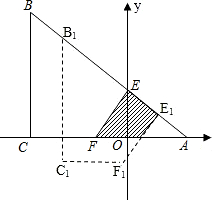 单位长度,平移中四边形BCFE与△AEF重叠的面积为S.
单位长度,平移中四边形BCFE与△AEF重叠的面积为S. ,与x轴相交于点F.
,与x轴相交于点F.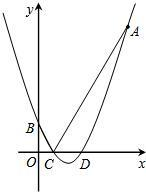

 s向C点匀速移动,已知AC=4cm,BC=12cm,
s向C点匀速移动,已知AC=4cm,BC=12cm,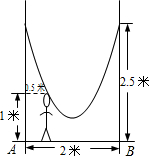 坐标系,根据题中提供的信息,求绳子所在抛物线的函数关系式;
坐标系,根据题中提供的信息,求绳子所在抛物线的函数关系式;