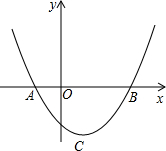
题目内容
已知抛物线y=-
x2+bx+c与x轴交于A、B,与y轴交于点C,连结AC、BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF.若S△OBC=8,AC=BC
(1)求抛物线的解析式;
(2)求证:BF⊥AB;
(3)求∠FBE;
(4)当D点沿x轴正方向移动到点B时,点E也随着运动,则点E所走过的路线长是______.

| 1 |
| 4 |
(1)求抛物线的解析式;
(2)求证:BF⊥AB;
(3)求∠FBE;
(4)当D点沿x轴正方向移动到点B时,点E也随着运动,则点E所走过的路线长是______.

(1)如图,∵AC=BC,
∴该抛物线的对称轴是y轴,则b=0.
∴C(0,c),B(
,0).
∵S△OBC=8,
∴
OC•OB=
×c×
=8,解得c=4(c>0).
故该抛物线的解析式为y=-
x2+4;
(2)证明:由(1)得到抛物线的解析式为y=-
x2+4;
令y=0,得x1=4,x2=-4,
∴A(-4,0),B(4,0),
∴OA=OB=OC,
∴△ABC是等腰直角三角形;
如图,又∵四边形CDEF是正方形,
∴AC=BC,CD=CF,∠ACD=∠BCF,
在△ACD和△BCF中
,
∴△ACD≌△BCF(SAS),
∴∠CBF=∠CAD=45°,
∴∠ABF=∠ABC+∠CBF=90°,
∴BF⊥AB;
(3)如图,连接BE,过点E作EM⊥x轴于点M.
易证△ODC≌△DME,则DM=OC=4,OD=EM.
∵OD=OB-BD=4-BD=DM-BD=BM,
∴BM=EM.
∵∠EMB=90°,
∴∠MBE=∠MEB=45°;
由(2)知,BF⊥AB,
∴∠FBE=∠FBM-∠MBE=45°;
(4)由(3)知,点E在定直线上,当点D沿x轴正方向移动到点B时,点E所走过的路程长等于BC=4
.故答案是:4
.
∴该抛物线的对称轴是y轴,则b=0.
∴C(0,c),B(
| 4c |
∵S△OBC=8,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 4c |
故该抛物线的解析式为y=-
| 1 |
| 4 |
(2)证明:由(1)得到抛物线的解析式为y=-
| 1 |
| 4 |
令y=0,得x1=4,x2=-4,
∴A(-4,0),B(4,0),
∴OA=OB=OC,
∴△ABC是等腰直角三角形;
如图,又∵四边形CDEF是正方形,
∴AC=BC,CD=CF,∠ACD=∠BCF,
在△ACD和△BCF中
|
∴△ACD≌△BCF(SAS),
∴∠CBF=∠CAD=45°,
∴∠ABF=∠ABC+∠CBF=90°,
∴BF⊥AB;

(3)如图,连接BE,过点E作EM⊥x轴于点M.
易证△ODC≌△DME,则DM=OC=4,OD=EM.
∵OD=OB-BD=4-BD=DM-BD=BM,
∴BM=EM.
∵∠EMB=90°,
∴∠MBE=∠MEB=45°;
由(2)知,BF⊥AB,
∴∠FBE=∠FBM-∠MBE=45°;
(4)由(3)知,点E在定直线上,当点D沿x轴正方向移动到点B时,点E所走过的路程长等于BC=4
| 2 |
| 2 |

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目


 B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.