题目内容
如图,抛物线:y=
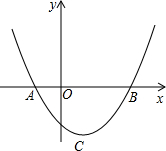
x2+bx+c与x轴交于A、B(A在B左侧),顶点为C(1,-2),
(1)求此抛物线的关系式;并直接写出点A、B的坐标.
(2)求过A、B、C三点的圆的半径.
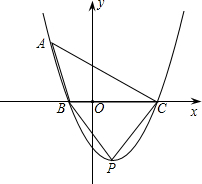
(3)在抛物线上找点P,在y轴上找点E,使以A、B、P、E为顶点的四边形是平行四边形,求点P、E的坐标.
| 1 |
| 2 |
(1)求此抛物线的关系式;并直接写出点A、B的坐标.
(2)求过A、B、C三点的圆的半径.
(3)在抛物线上找点P,在y轴上找点E,使以A、B、P、E为顶点的四边形是平行四边形,求点P、E的坐标.

(1)∵抛物线y=
x2+bx+c的顶点为C(1,-2),
∴-
=-
=1,
解得b=-1,
=
=-2,
解得c=-
,
∴抛物线解析式为y=
x2-x-
,
令y=0,则
x2-x-
=0,
解得x1=-1,x2=3,
∴点A、B的坐标为:A(-1,0)、B(3,0);
(2)∵A(-1,0)、B(3,0)、C(1,-2),
∴AB=3-(-1)=4,
AC=
=2
,
BC=
=2
,
∴AB2=16,AC2+BC2=8+8=16,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,AB是直径,
故半径为2;
(3)①当AB是平行四边形的边时,PE=AB=4,且点P、E的纵坐标相等,
∴点P的横坐标为4或-4,
∴y=
×42-4-
=
,
或y=
×42+4-
=
,
∴点P、E的坐标为P1(4,
)、E1(0,
)或P2(-4,
)、E2(0,
),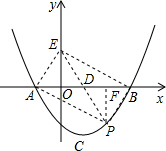
②如图,当AB是平行四边形的对角线时,PE平分AB,
∴PE与x轴的交点坐标D(1,0),
过点P作PF⊥AB,则OD=FD,
∴点F的坐标为(2,0),
∴点P的横坐标为2,
y=
×22-2-
=-
,
∴点P的纵坐标为
,
∴点P、E的坐标为P3(2,-
)、E3(0,
),
综上所述,点P、E的坐标为:P1(4,
)、E1(0,
)或P2(-4,
)、E2(0,
)或P3(2,-
)、E3(0,
).
| 1 |
| 2 |
∴-
| b |
| 2a |
| b | ||
2×
|
解得b=-1,
| 4ac-b2 |
| 4a |
4×
| ||
4×
|
解得c=-
| 3 |
| 2 |
∴抛物线解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
令y=0,则
| 1 |
| 2 |
| 3 |
| 2 |
解得x1=-1,x2=3,
∴点A、B的坐标为:A(-1,0)、B(3,0);
(2)∵A(-1,0)、B(3,0)、C(1,-2),
∴AB=3-(-1)=4,
AC=
| (-1-1)2+[0-(-2)]2 |
| 2 |
BC=
| (3-1)2+[0-(-2)]2 |
| 2 |
∴AB2=16,AC2+BC2=8+8=16,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,AB是直径,
故半径为2;
(3)①当AB是平行四边形的边时,PE=AB=4,且点P、E的纵坐标相等,
∴点P的横坐标为4或-4,
∴y=
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
或y=
| 1 |
| 2 |
| 3 |
| 2 |
| 21 |
| 2 |
∴点P、E的坐标为P1(4,
| 5 |
| 2 |
| 5 |
| 2 |
| 21 |
| 2 |
| 21 |
| 2 |

②如图,当AB是平行四边形的对角线时,PE平分AB,
∴PE与x轴的交点坐标D(1,0),
过点P作PF⊥AB,则OD=FD,
∴点F的坐标为(2,0),
∴点P的横坐标为2,
y=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴点P的纵坐标为
| 3 |
| 2 |
∴点P、E的坐标为P3(2,-
| 3 |
| 2 |
| 3 |
| 2 |
综上所述,点P、E的坐标为:P1(4,
| 5 |
| 2 |
| 5 |
| 2 |
| 21 |
| 2 |
| 21 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |

练习册系列答案
相关题目


 为直径作⊙D,设⊙D的半径为2.
为直径作⊙D,设⊙D的半径为2.