题目内容
如图,已知抛物线y=ax2+b经过点A(4,4)和点B(0,-4).C是x轴上的一个动点.
(1)求抛物线的解析式;
(2)若点C在以AB为直径的圆上,求点C的坐标;
(3)将点A绕C点逆时针旋转90°得到点D,当点D在抛物线上时,求出所有满足条件的点C的坐标.

(1)求抛物线的解析式;
(2)若点C在以AB为直径的圆上,求点C的坐标;
(3)将点A绕C点逆时针旋转90°得到点D,当点D在抛物线上时,求出所有满足条件的点C的坐标.

(1)∵抛物线y=ax2+b的图象经过点A(4,4)和点B(0,-4),
∴
,解得:
,
∴抛物线的解析式为:y=
x2-4;…(3分)
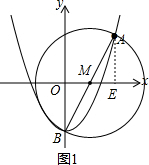
(2)过点A作AE⊥x轴于E,连接AB交x轴于点M,
OB=AE=4,∠MOB=∠AEM=90°,∠OMB=∠AME,
∴在△OMB与△EMA中,
∴
∴△OMB≌△EMA,
∴MB=MA,OM=ME=
OE=2,
∴以M为圆心,MB为半径的⊙M,即为以AB为直径的圆.
由勾股定理得MB=
=
=2
,
∴点C的坐标为(2-2
,0),(2+2
,0).
(3)如图2,当点C在点(4,0)的右侧时,
作AE⊥x轴于E,DF⊥x轴于F,
∵△ACD为等腰直角三角形,
∴AC=DC,∠ACD=90°,即∠ACF+∠DCF=90°,
∵∠FDC+∠DCF=90°,
∴∠ACF=∠FDC,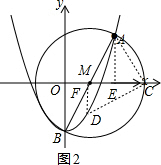
又∵∠DFC=∠AEC=90°,
在△DFC与△CEA中,
∴△DFC≌△CEA,
∴EC=DF,FC=AE,
∵A(4,4),
∴AE=OE=4,
∴FC=OE,即OF+EF=CE+EF,
∴OF=CE,
∴OF=DF,
当点C与点(4,0)的重合时,点D与原点重合;
当点C在点(4,0)的左侧时,同理可得OF=DF;
∴综上所述,点D在直线y=-x的图象上.
设点C的坐标为(m,0),
则点D的坐标为(m-4,4-m),(13分)
又∵点D在抛物线y=
x2-4的图象上,
∴4-m=
(m-4)2-4,
解得:m1=0,m2=6,
∴当点C的坐标为(6,0)或(0,0)时,
点D落在抛物线y=
x2-4的图象上.
∴
|
|
∴抛物线的解析式为:y=
| 1 |
| 2 |
(2)过点A作AE⊥x轴于E,连接AB交x轴于点M,
OB=AE=4,∠MOB=∠AEM=90°,∠OMB=∠AME,
∴在△OMB与△EMA中,
∴
|
∴△OMB≌△EMA,
∴MB=MA,OM=ME=
| 1 |
| 2 |
∴以M为圆心,MB为半径的⊙M,即为以AB为直径的圆.
由勾股定理得MB=
| OM2+OB2 |
| 22+42 |
| 5 |
∴点C的坐标为(2-2
| 5 |
| 5 |
(3)如图2,当点C在点(4,0)的右侧时,
作AE⊥x轴于E,DF⊥x轴于F,
∵△ACD为等腰直角三角形,
∴AC=DC,∠ACD=90°,即∠ACF+∠DCF=90°,
∵∠FDC+∠DCF=90°,
∴∠ACF=∠FDC,

又∵∠DFC=∠AEC=90°,
在△DFC与△CEA中,
|
∴△DFC≌△CEA,
∴EC=DF,FC=AE,
∵A(4,4),
∴AE=OE=4,
∴FC=OE,即OF+EF=CE+EF,
∴OF=CE,
∴OF=DF,
当点C与点(4,0)的重合时,点D与原点重合;
当点C在点(4,0)的左侧时,同理可得OF=DF;
∴综上所述,点D在直线y=-x的图象上.
设点C的坐标为(m,0),
则点D的坐标为(m-4,4-m),(13分)
又∵点D在抛物线y=
| 1 |
| 2 |
∴4-m=
| 1 |
| 2 |
解得:m1=0,m2=6,
∴当点C的坐标为(6,0)或(0,0)时,
点D落在抛物线y=
| 1 |
| 2 |


练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目










