题目内容
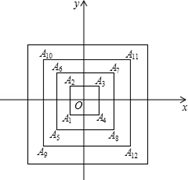
在平面直角坐标系中，对于平面内任意一点（x，y），若规定以下两种变换：
①f (x，y) = (x+2，y)；②g(x，y) = (?x ，?y)，
例如按照以上变换有：f(1，1)=(3，1)；g( f (1，1)) =" g" (3，1) = (?3，?1)．
如果有数a、b，使得f (g(a，b )) = (b，?a)，则g(f(a+b，a?b)) = ．
①f (x，y) = (x+2，y)；②g(x，y) = (?x ，?y)，
例如按照以上变换有：f(1，1)=(3，1)；g( f (1，1)) =" g" (3，1) = (?3，?1)．
如果有数a、b，使得f (g(a，b )) = (b，?a)，则g(f(a+b，a?b)) = ．
（?４，０）
试题分析：先读懂题中变换法则结合f ( g(a，b )) = (b，a )求得a、b的值，即可求得结果.
∵f ( g(a，b )) =" f" (?a，?b) = (?a+2，?b) = (b，?a)
∴
，解得
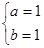
∴g(f(a+b，a?b)) = g(f(2，0)) = g(4，0) =（?４，０）.
点评：本题一种新型运算方式，解决的关键是理解相关定义，难点是确定运算顺序．
练习册系列答案
相关题目
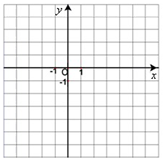
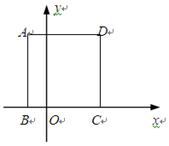
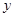轴上找一点C，使得AC＋BC的值最小；
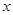轴上找一点D，使得AD－BD的值最大．
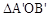的位置，点B的横坐标为2，则点
的坐标为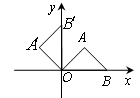
)
)
，
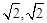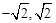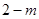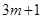）在x轴上，则
=________．
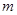