题目内容
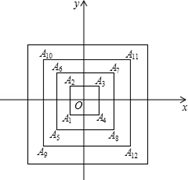
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是

| A.(13,13) | B.(﹣13,﹣13) | C.(14,14) | D.(﹣14,﹣14) |
C
试题分析:观察图象,每四个点一圈进行循环,每一圈第一个点在第三象限,根据点的脚标与坐标寻找规律.
∵55=4×13+3,
∴A55与A3在同一象限,即都在第一象限,
根据题中图形中的规律可得:
3=4×0+3,A3的坐标为(0+1,0+1),即A3(1,1),
7=4×1+3,A7的坐标为(1+1,1+1),A7(2,2),
11=4×2+3,A11的坐标为(2+1,2+1),A11(3,3);
…
55=4×13+3,A55(14,14),A55的坐标为(13+1,13+1);
故选C.
点评:解答此题的关键是首先确定点所在的大致位置及所在的正方形,然后就可以进一步推得点的坐标.

练习册系列答案
相关题目


 ABC的面积。
ABC的面积。 的顶点坐标为
的顶点坐标为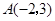 、
、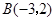 、
、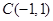 .
.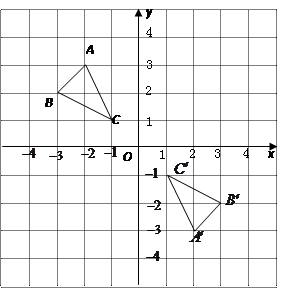
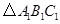 ;
;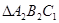 ;
; 与
与