题目内容
已知在平面直角坐标系中,点A,B的坐标分别为A(2,-5),
B(5,1).在同一个坐标系内画出满足下列条件的点(保留画图痕迹),并求出该点的坐标.
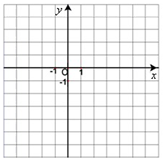
(1)在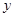 轴上找一点C,使得AC+BC的值最小;
轴上找一点C,使得AC+BC的值最小;
(2)在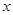 轴上找一点D,使得AD-BD的值最大.
轴上找一点D,使得AD-BD的值最大.
B(5,1).在同一个坐标系内画出满足下列条件的点(保留画图痕迹),并求出该点的坐标.

(1)在
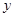 轴上找一点C,使得AC+BC的值最小;
轴上找一点C,使得AC+BC的值最小;(2)在
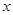 轴上找一点D,使得AD-BD的值最大.
轴上找一点D,使得AD-BD的值最大.(1)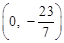 (2)
(2)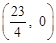
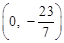 (2)
(2)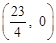
试题分析:(1) C点如图
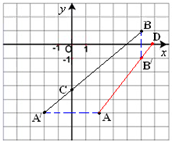
(或作B关于y轴的对称点B′,连结AB′交y轴于点C)
解得A′B直线解析式:
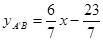 或
或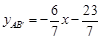 )
)∴点C的坐标为
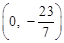
(2) D点如图(作点B关于x轴的对称点B′,连结AB’延长交x轴于D)
(理由:若A,B′,D三点不共线,根据三角形两边之差小于第三条边可得:AD-B′D<AB′
∴当A,B′,D三点共线时,AD-B′D =AB′,此时AD-B′D有最大值,最大值为AB′的长度. 此时,点D在直线AB′上)
根据题意由A(2,-5),B′(5,-1)代入可得
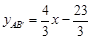 ,
,∴当AD-BD有最大值时,点D的坐标为
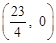
点评:该题是常考题,看似考最短线段,其实是考学生对作最短线段方法的思路,通过作某一点的对称点,应用两点之间,线段最短的性质来判断。

练习册系列答案
相关题目
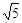
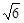

 的顶点坐标为
的顶点坐标为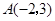 、
、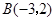 、
、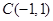 .
.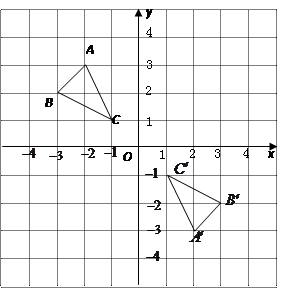
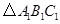 ;
;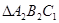 ;
;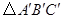 与
与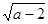 +(b-3)2=0,(c-4)2≤0.
+(b-3)2=0,(c-4)2≤0.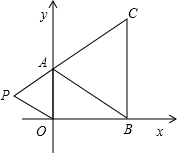
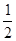 ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;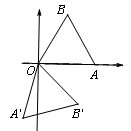
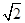 ,
,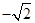 )
)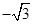 ,
, 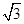 )
)