题目内容
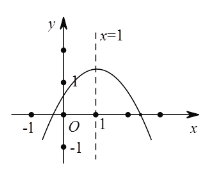
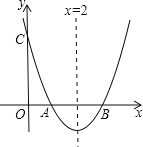
【题目】已知如图1，在以O为原点的平面直角坐标系中，抛物线y＝
x2+bx+c与x轴交于A，B两点，与y轴交于点C（0，﹣1），连接AC，AO＝2CO，直线l过点G（0，t）且平行于x轴，t＜﹣1．
（1）求抛物线对应的二次函数的解析式；
（2）若D（﹣4，m）为抛物线y＝x2+bx+c上一定点，点D到直线l的距离记为d，当d＝DO时，求t的值．
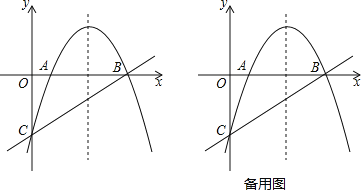
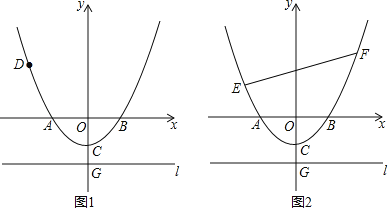
（3）如图2，若E（﹣4，m）为上述抛物线上一点，在抛物线上是否存在点F，使得△BEF是直角三角形，若存在求出点F的坐标，若不存在说明理由．
【答案】（1）y＝
x2﹣1；（2）t＝﹣2；（3）存在点F，使得△BEF是直角三角形，点F的坐标为（6，8）．
【解析】
（1）根据点C坐标，可得c＝﹣1，然后根据AO＝2CO，可得出点A坐标，将点A坐标代入求出b值，即可得出函数解析式；
（2）根据抛物线的解析式求得D的坐标为（﹣4，3），即可求得OD＝5，结合D的纵坐标3，即可求得t＝﹣2．
（3）分两种情况讨论：当B点为直角顶点时，则BF⊥BE，根据直线BE的解析式求得直线BF的解析式，然后和抛物线解析式联立方程，求得交点坐标即可；当F点为直角顶点时，求得到直线BE上距离为最大值的点P的坐标，然后求得线段BE的中点Q到P点的距离，和BE的一半比较即可判断以BE为直径的圆与抛物线无交点，故此种情况不存在，综上求得F点的坐标．
（1）∵C（0，﹣1），
∴y＝x2+bx﹣1，
又∵AO＝2OC，
∴点A坐标为（﹣2，0），
代入得：1﹣2b﹣1＝0，
解得：b＝0，
∴解析式为：y＝x2﹣1；
（2）∵D（﹣4，m）为抛物线y＝x2﹣1上一定点，
∴m＝×16﹣1＝3，
∴D（﹣4，3），
∴OD＝
＝5，
∴d＝5，
∴t＝﹣（5﹣3）＝﹣2；
（3）点E（﹣4，m）在抛物线y＝x2﹣1的上，
∴m＝3，
∴E（﹣4，3），
∵B（2，0），
∴直线BE为y＝﹣
x+1，
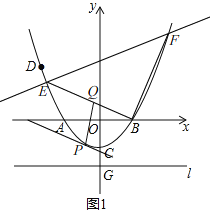
如图1，当B点为直角顶点时，则BF⊥BE，
∴直线BF的斜率为2，
设直线BF的解析式为y＝2x+n，
把B（2，0）代入得2×2+n＝0，
∴n＝﹣4，
∴直线BF的解析式为y＝2x﹣4，
解
得
或
，
∴F（6，8）；
当F点为直角顶点时，
设BE的平行线y＝﹣x+b与抛物线有且只有一个交点P，
∴﹣x+b＝x2﹣1，
整理得x2+2x﹣4b﹣4＝0，
∴
＝4+4（4b+4）＝0，
解得b＝﹣
，
∴平行线为y＝﹣
﹣，
∴x2+2x+1＝0，
解得x＝﹣1，
∴y＝﹣
，
∴平行线与抛物线的交点P为（﹣1，﹣），
∵B（2，0），E（﹣4，3），
∴BE＝
，
∴BE的中点Q为（﹣1，
），
∴QP＝+＝
＜
＝BE，
∴此种情况不存在，
故在抛物线上存在点F，使得△BEF是直角三角形，点F的坐标为（6，8）．
