题目内容
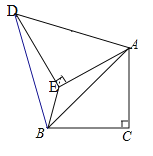
【题目】如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是_____.
【答案】4πcm2.
【解析】
当该圆为三角形内切圆时面积最大,设内切圆半径为r,则该三角形面积可表示为:![]() r(AB+AC+BC)=21r,过点A作AD⊥BC交BC的延长线于点D,利用勾股定理可求出AD,易得三角形ABC的面积,求出r即可求得圆的面积.
r(AB+AC+BC)=21r,过点A作AD⊥BC交BC的延长线于点D,利用勾股定理可求出AD,易得三角形ABC的面积,求出r即可求得圆的面积.
如图1所示,设三角形内切圆半径为r,
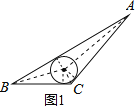
则S△ABC=![]() r(AB+BC+AC)=
r(AB+BC+AC)=![]() r×42=21r,
r×42=21r,
过点A作AD⊥BC交BC的延长线于点D,如图2,
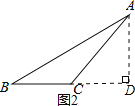
设CD=x,
在Rt△ABD中,由勾股定理得:AD2=AB2﹣BD2=400﹣(7+x)2,
在Rt△ACD中,AD2=AC2﹣x2=225﹣x2,
∴400﹣(7+x)2=225﹣x2,
解得:x=9,
∴AD=12,
∴S△ABC=![]() BC×AD=
BC×AD=![]() ×7×12=42,
×7×12=42,
∴21r=42,
∴r=2,
该圆的最大面积为:S=πr2=4π(cm2),
故答案为:4πcm2.

练习册系列答案
相关题目