题目内容
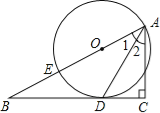
【题目】如图,在正方形ABCD的对角线AC上取点E,使得∠CDE=15°,连接BE.延长BE到F,连接CF,使得CF=BC.
(1)求证:DE=BE;
(2)求证:EF=CE+DE.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由正方形的性质可以得出AB=AD,∠BAC=∠DAC=45°,通过证明△ABE≌△ADE,就可以得出结论;
(2)在EF上取一点G,使EG=EC,连结CG,再通过条件证明△DEC≌△FGC就可以得出结论.
试题解析:(1)∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠ADC=90°,
∠BAC=∠DAC=45°.
∵在△ABE和△ADE中,  ,
,
∴△ABE≌△ADE(SAS),
∴BE=DE.
(2)在EF上取一点G,使EG=EC,连结CG,

∵△ABE≌△ADE,
∴∠ABE=∠ADE.
∴∠CBE=∠CDE,
∵BC=CF,∴∠CBE=∠F,
∵∠CDE=15°,∴∠CBE=15°,
∴∠CEG=60°.
∵CE=GE,∴△CEG是等边三角形.
∴∠CGE=60°,CE=GC,
∴∠GCF=45°,
∴∠ECD=GCF.
∵在△DEC和△FGC中,  ,
,
∴△DEC≌△FGC(SAS),
∴DE=GF.
∵EF=EG+GF,
∴EF=CE+ED.

练习册系列答案
相关题目