题目内容
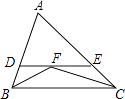
【题目】如图,在ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据全等三角形的判定方法,判断出△ADE≌△CBF,即可推得DE=BF.
(2)首先判断出DE∥BF;然后根据一组对边平行且相等的四边形是平行四边形,推得四边形DEBF是平行四边形即可.
试题解析:(1)∵四边形ABCD是平行四边形,∴AD∥CB,AD=CB,∴∠DAE=∠BCF,在△ADE和△CBF中,∵AD=CB,∠DAE=∠BCF,AE=CF,∴△ADE≌△CBF,∴DE=BF.
(2)由(1),可得∴△ADE≌△CBF,∴∠ADE=∠CBF,∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,∴∠DEF=∠BFE,∴DE∥BF,又∵DE=BF,∴四边形DEBF是平行四边形.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目