题目内容
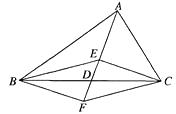
【题目】如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,那么下列结论:①△BDF、△CEF都是等腰三角形;②DE=DB+CE;③AD+DE+AE=AB+AC;④BF=CF.正确的有 . 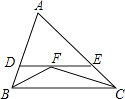
【答案】①②③
【解析】解:①∵BF是∠ABC的角平分线, ∴∠ABF=∠CBF,
又∵DE∥BC,
∴∠CBF=∠DFB,
∴DB=DF即△BDF是等腰三角形,
同理∠ECF=∠EFC,
∴EF=EC,
∴△BDF,△CEF都是等腰三角形;
∵∠B、∠C的角平分线交于点F,
∴∠DBF=∠CBF(设为α),∠ECF=∠BCF(设为β);
∵DE∥BC,
∴∠DFB=∠CBF=α,∠EFC=∠BCF=β;
∴∠DBF=∠DFB,∠EFC=∠ECF,
∴DB=DF,EF=EC;
∴DE=DB+CE,AD+DE+AE=AB+AC,②③正确;
AB和AC不一定相等,∴BF和CF不一定相等.故④错误
所以答案是:①②③
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目
【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 | 种植B类蔬菜面积 | 总收入 |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.