题目内容
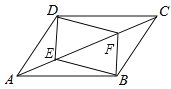
【题目】如图所示,一块等腰直角三角形铁板,通过切割焊接成一个含有45°角的平行四边形,设计一种简要的方案并给出正确的理由. 
【答案】解:如图,取AC、BC的中点E、D,连接ED,沿ED切割,固定点E,△ECD旋转180°使C点与A点重合即可. 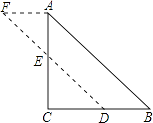
理由:在Rt△ABC中,
∵AC=BC,∠B=45°,
又∵E、D分别是AC、BC的中点,
∴EC=DC
∴∠CED=∠CDE=45°
∴∠AEF=∠CED=45°
∴∠AEF+∠AED=∠CED+∠AED=180°
∴F、E、D在一条直线上.
又∵∠EAF=∠C=90°
∴AF∥CD.
又∵AF=CD=DB,
∴四边形AFDB是平行四边形,且∠B=45°
【解析】∵这是一块等腰直角三角形铁板,已经包含45°的角.∴应用到题中45°的角,利用全等进行割补,应遵循简单易行的原则.
【考点精析】掌握等腰直角三角形和平行四边形的判定与性质是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.

练习册系列答案
相关题目
【题目】某人购进一批苹果,到市场零售,已知销售额y(元)与卖出的苹果数量x(千克)的关系如表所示:则y与x之间的关系式为__________
数量x(千克) | 2 | 3 | 4 | 5 | … |
销售额y(元) | 7.2 | 10.8 | 14.4 | 18.0 | … |