题目内容
【题目】如图,在△ABC中,∠CAB=130°,AB、AC的垂直平分线分别交BC于点E、F则∠EAF等于( ) 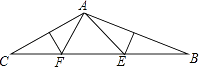
A.60°
B.70°
C.80°
D.90°
【答案】C
【解析】解:∵∠CAB=130°, ∴∠B+∠C=180°﹣130°=50°,
∵AB、AC的垂直平分线分别交BC于点E、F,
∴AE=BE,AF=CF,
∴∠BAE=∠B,∠CAF=∠C,
由三角形的外角性质得,∠AEF=∠B+∠BAE=2∠B,∠AFE=∠C+∠CAF=2∠C,
所以,∠AEF+∠AFE=2(∠B+∠C)=2×50°=100°,
所以,∠EAF=180°﹣(∠AEF+∠AFE)=180°﹣100°=80°.
故选C.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.

练习册系列答案
相关题目
【题目】某人购进一批苹果,到市场零售,已知销售额y(元)与卖出的苹果数量x(千克)的关系如表所示:则y与x之间的关系式为__________
数量x(千克) | 2 | 3 | 4 | 5 | … |
销售额y(元) | 7.2 | 10.8 | 14.4 | 18.0 | … |