��Ŀ����
����Ŀ����֪����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ���㣨�����
��һ���㣨�����![]() ��
��![]() �غϣ�����
�غϣ�����![]() Ϊ����������
����������![]() ������
������![]() .
.
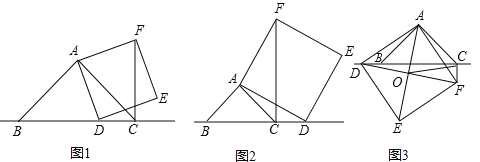
��1����ͼ1������![]() ���߶�
���߶�![]() ��ʱ����ֱ��д����
��ʱ����ֱ��д����![]() ��
��![]() ��
��![]() �����߶�֮���������ϵΪ________.
�����߶�֮���������ϵΪ________.
��2����ͼ2������![]() ���߶�
���߶�![]() ���ӳ�����ʱ��������������.��1���еĽ����Ƿ���Ȼ�������������������֤������������������д����ȷ�Ľ��ۣ�������֤��.
���ӳ�����ʱ��������������.��1���еĽ����Ƿ���Ȼ�������������������֤������������������д����ȷ�Ľ��ۣ�������֤��.
��3����ͼ3������![]() ���߶�
���߶�![]() �ķ����ӳ�����ʱ���ҵ�
�ķ����ӳ�����ʱ���ҵ�![]() ��
��![]() �ֱ���ֱ��
�ֱ���ֱ��![]() �����࣬������������.��ֱ��д����
�����࣬������������.��ֱ��д����![]() ��
��![]() ��
��![]() �����߶�֮���������ϵ______________.
�����߶�֮���������ϵ______________.
���𰸡���1��![]() ����2������������ȷ�Ľ��ۣ�
����2������������ȷ�Ľ��ۣ�![]() ������������3��
������������3��![]() .
.
��������
��1��������ABC�ǵ���ֱ�������Σ�����SAS����֤����BAD�ա�CAF���Ӷ�֤��CF=BD���ݴ˼���֤�ã�
��2��ͬ��1����ͬ������SAS����֤�á�BAD�ա�CAF���Ӷ�֤��BD=CF�����ɵõ�CF-CD=BC��
��3������֤����BAD�ա�CAF����FCD��ֱ�������Σ�Ȼ���������������ã�
�⣺��1���ߡ�BAC=90�㣬��ABC=45�㣬
���ACB=��ABC=45�㣬
��AB=AC��
���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬
�ߡ�BAD=90��-��DAC����CAF=90��-��DAC��
���BAD=��CAF��
���ڡ�BAD�͡�CAF�У�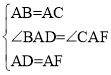 ��
��
���BAD�ա�CAF��SAS����
��BD=CF��
��BD+CD=BC��
��CF+CD=BC��
��2��������
![]() ���������£���ͼ2
���������£���ͼ2
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() .
.
���ı���![]() Ϊ�����Σ�
������
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() .
.
��3�����ݢ٢ڿ�֪��BAD�ա�CAF��SAS����
��BD=CF��DC=BD+BC��
��BC=CD��CF.