Question

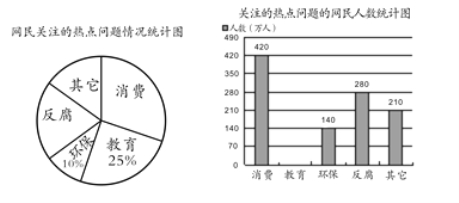
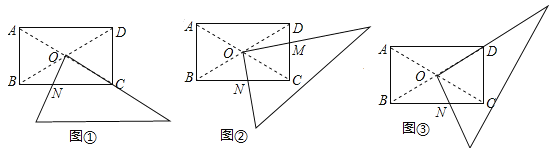
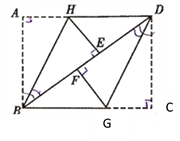
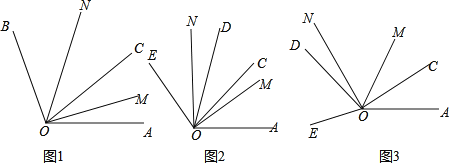
【题目】（1）如图1，∠AOC＝α，∠BOC＝β，若OM平分∠AOC，ON平分∠BOC，则∠MON＝　 　（用含α、β的式子表示）；

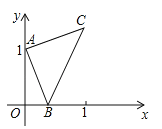
（2）如图2，若将∠BOC绕点O逆时针旋转30°后得到∠EOD，OM平分∠AOD，ON平分∠COE，求∠MON的度数（用含α、β的式子表示）；

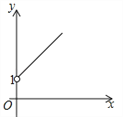
（3）若∠BOC旋转90°至图3的位置，其他条件不变，则∠MON的度数是　 　（用含α、β的式子表示）．

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）∠MON＝∠COM+CON，根据已知条件，求出∠COM和CON即可；

（2）由已知可得∠COD＝30°，∠DOE＝β，∠AOD＝∠AOC+∠COD＝α+30°，∠COE＝∠COD+DOE＝β+30°，根据∠MON＝∠MOD+∠NOC﹣∠COD，代入数值求出即可；

（3）由已知可得∠COD＝90°，∠DOE＝β，∠AOD＝∠AOC+COD＝90°+α，∠COE＝∠COD+DOE＝β+90°，根据∠MON＝∠MOD+∠NOC﹣∠COD，代入数值求出即可．

解：（1）∵∠AOC＝α，∠BOC＝β，OM平分∠AOC，ON平分∠BOC，

∴∠COM＝ ，∠CON＝，

∴∠MON＝∠COM+CON＝；

故答案为：；

（2）由题意可知：∠COD＝30°，∠DOE＝β，∠AOD＝∠AOC+∠COD＝α+30°，∠COE＝∠COD+DOE＝β+30°，

∵OM平分∠AOD，ON平分∠COE，

∴∠MOD＝∠AOD，∠NOC＝，

∴∠MON＝∠MOD+∠NOC﹣∠COD＝＝；

（3）由题意可得，∠COD＝90°，∠DOE＝β，∠AOD＝∠AOC+COD＝90°+α，∠COE＝∠COD+DOE＝β+90°，

∵OM平分∠AOD，ON平分∠COE，

∴∠MOD＝∠AOD，∠NOC＝，

∴∠MON＝∠MOD+∠NOC﹣∠COD＝＝，

故答案为：．