Question

【题目】已知矩形，为边上一点，，点从点出发，以每秒个单位的速度沿着边向终点运动，连接，设点运动的时间为秒，则当的值为__________时，是以为腰的等腰三角形．

Answer 1

【答案】或

【解析】

根据矩形的性质求出∠D=90°，AB=CD=8，求出DE后根据勾股定理求出AE；过E作EM⊥AB于M，过P作PQ⊥CD于Q，求出AM=DE=3，当EP=EA时，AP=2DE=6，即可求出t；当AP=AE=5时，求出BP=3，即可求出t；当PE=PA时，则x2=（x-3）2+42，求出x，即可求出t．

∵四边形ABCD是长方形，

∴∠D=90°，AB=CD=8，

∵CE=5，

∴DE=3，

在Rt△ADE中,∠D=90°,AD=4,DE=3,由勾股定理得：AE=5

过E作EM⊥AB于M，过P作PQ⊥CD于Q，

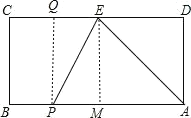
则AM=DE=3，

若△PAE是等腰三角形，则有三种可能：

当EP=EA时，AP=2DE=6，

所以t==2；

当AP=AE=5时，BP=85=3，

所以t=3÷1=3；

当PE=PA时,设PA=PE=x,BP=8x,则EQ=5(8x)=x3，

则

解得：x=，

则t=(8)÷1=，

综上所述t=2或时，△PAE为等腰三角形。

故答案为：2或.