ЬтФПФкШн
ЁОЬтФПЁПвбжЊЪ§жсЩЯЃЌЕуOЮЊдЕуЃЌЕуAЖдгІЕФЪ§ЮЊ9ЃЌЕуBЖдгІЕФЪ§ЮЊbЃЌЕуCдкЕуBгвВрЃЌГЄЖШЮЊ2ИіЕЅЮЛЕФЯпЖЮBCдкЪ§жсЩЯвЦЖЏЃЎ
![]()
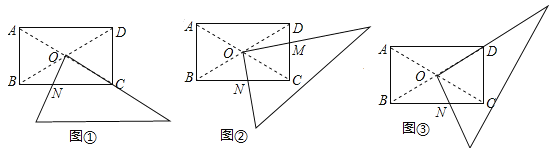
ЃЈ1ЃЉШчЭМЃЌЕБЯпЖЮBCдкOЁЂAСНЕужЎМфвЦЖЏЕНФГвЛЮЛжУЪБЃЌЧЁКУТњзуЯпЖЮACЃНOBЃЌЧѓДЫЪБbЕФжЕЃЛ
ЃЈ2ЃЉЕБЯпЖЮBCдкЪ§жсЩЯбиЩфЯпAOЗНЯђвЦЖЏЕФЙ§ГЬжаЃЌШєДцдкACЉOBЃН![]() ABЃЌЧѓДЫЪБТњзуЬѕМўЕФbЕФжЕЃЛ
ABЃЌЧѓДЫЪБТњзуЬѕМўЕФbЕФжЕЃЛ
ЃЈ3ЃЉЕБЯпЖЮBCдкЪ§жсЩЯвЦЖЏЪБЃЌТњзуЙиЯЕЪН|ACЉOB|ЃН![]() |ABЉOC|ЃЌдђДЫЪБbЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁ
|ABЉOC|ЃЌдђДЫЪБbЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁ
ЁОД№АИЁПЃЈ1ЃЉ3.5ЃЛЃЈ2ЃЉ![]() ЛђЉ12ЃЛЃЈ3ЃЉbЁмЉ2ЛђbЁн9ЛђbЃН3.5
ЛђЉ12ЃЛЃЈ3ЃЉbЁмЉ2ЛђbЁн9ЛђbЃН3.5
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтПЩжЊBЕуБэЪОЕФЪ§БШЕуCЖдгІЕФЪ§Щй2ЃЌНјвЛВНгУbБэЪОГіACЁЂOBжЎМфЕФОрРыЃЌСЊСЂЗНГЬЧѓЕУbЕФЪ§жЕМДПЩЃЛ
ЃЈ2ЃЉЗжБ№гУbБэЪОГіACЁЂOBЁЂABЃЌНјвЛВНРћгУACЉ0BЃН![]() ABНЈСЂЗНГЬЧѓЕУД№АИМДПЩЃЛ
ABНЈСЂЗНГЬЧѓЕУД№АИМДПЩЃЛ
ЃЈ3ЃЉЗжБ№гУbБэЪОГіACЁЂOBЁЂABЁЂOCЃЌНјвЛВНРћгУ|ACЉOB|ЃН![]() |ABЉOC|НЈСЂЗНГЬЧѓЕУД№АИМДПЩЃЎ
|ABЉOC|НЈСЂЗНГЬЧѓЕУД№АИМДПЩЃЎ
НтЃКЃЈ1ЃЉгЩЬтвтЕУЃК
9ЉЃЈb+2ЃЉЃНbЃЌ
НтЕУЃКbЃН3.5ЃЎ
Д№ЃКЯпЖЮACЃНOBЃЌДЫЪБbЕФжЕЪЧ3.5ЃЎ
ЃЈ2ЃЉгЩЬтвтЕУЃК
Ђй9ЉЃЈb+2ЃЉЉbЃН![]() ЃЈ9ЉbЃЉЃЌ
ЃЈ9ЉbЃЉЃЌ
НтЕУЃКbЃН![]() ЃЎ
ЃЎ
Ђк9ЉЃЈb+2ЃЉ+bЃН![]() ЃЈ9ЉbЃЉЃЌ
ЃЈ9ЉbЃЉЃЌ
НтЕУЃКbЃНЉ12
Д№ЃКШєACЉ0BЃН![]() ABЃЌТњзуЬѕМўЕФbжЕЪЧ
ABЃЌТњзуЬѕМўЕФbжЕЪЧ![]() ЛђЉ12ЃЎ
ЛђЉ12ЃЎ
ЃЈ3ЃЉЂйЕБbЁн9ЪБЃЌACЃНb+2Љ9ЃЌOBЃНbЃЌABЃНbЉ9ЃЌOCЃНb+2ЃЌ
|ACЉOB|ЃН![]() |ABЉOC|ЃЌ
|ABЉOC|ЃЌ
|b+2Љ9Љb|ЃН7ЃЌ
![]() |ABЉOC|ЃН
|ABЉOC|ЃН![]() ЁС11ЃН7ЃЌ
ЁС11ЃН7ЃЌ
ЁрКуГЩСЂЃЛ
Ђк7ЁмbЃМ9ЪБЃЌ
|ACЉOB|ЃН![]() |ABЉOC|ЃЌ
|ABЉOC|ЃЌ
|b+2Љ9Љb|ЃН![]() |9ЉbЉЃЈb+2ЃЉ|ЃЌ
|9ЉbЉЃЈb+2ЃЉ|ЃЌ
НтЕУbЃНЉ2ЃЈЩсШЅЃЉЛђbЃН9ЃЈЩсШЅЃЉЃЛ
Ђл0ЁмbЃМ7ЪБЃЌ
|ACЉOB|ЃН![]() |ABЉOC|ЃЌ
|ABЉOC|ЃЌ
|9ЉЃЈb+2ЃЉЉb|ЃН![]() |9ЉbЉЃЈb+2ЃЉ|ЃЌ
|9ЉbЉЃЈb+2ЃЉ|ЃЌ
НтЕУbЃН![]() ЃН3.5ЃЎ
ЃН3.5ЃЎ
ЂмЉ2ЁмbЃМ0ЪБЃЌ
|9ЉЃЈb+2ЃЉ+b|ЃН![]() |9ЉbЉЃЈb+2ЃЉ|ЃЌ
|9ЉbЉЃЈb+2ЃЉ|ЃЌ
НтЕУbЃНЉ2ЛђbЃН9ЃЈЩсШЅЃЉЃЛ
ЂнЕБbЃМЉ2ЪБЃЌ
|9ЉЃЈb+2ЃЉ+b|ЃН![]() |9Љb+ЃЈb+2ЃЉ|КуГЩСЂЃЌ
|9Љb+ЃЈb+2ЃЉ|КуГЩСЂЃЌ
злЩЯЃЌbЕФШЁжЕЗЖЮЇЪЧbЁмЉ2ЛђbЁн9ЛђbЃН3.5ЃЎ
ЙЪД№АИЮЊЃКbЁмЉ2ЛђbЁн9ЛђbЃН3.5ЃЎ