题目内容
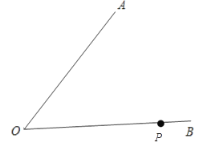
【题目】如图
，
是两条笔直的公路，点
是上的一个超市，现在想建一个服务区
，要求到两条公路的距离相等，且服务区到超市的距离最近，求作这个服务区．
【答案】图见解析
【解析】
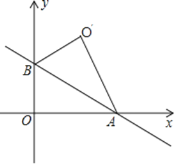
根据角平分线的判定，可知该服务区在∠O的平分线上，再根据垂线段最短，可知点P和服务区的连线垂直于∠O的平分线，故作出∠O的平分线，然后过点P作∠O的平分线的垂线，垂足即为所求．
解：以O为圆心，任意长度为半径作弧，分别交OA、OB于点D、E，分别以D、E为圆心，大于
DE的长为半径作弧，两弧交于点F，连接OF并延长，射线OF即为∠AOB的角平分线；
以P为圆心，大于P到OF的距离为半径作弧，交射线OF于G、H，分别以G、H为圆心，大于GH的长为半径作弧，两弧在射线OF上方交于点M，连接PM，与射线OF的交点即为服务区，此时PM⊥OF．
根据角平分线的判定和垂线段最短，这个服务区即为所求．
练习册系列答案
53随堂测系列答案
相关题目
