Question

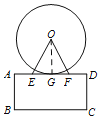
【题目】如图①是长春新地标一一摩天活力城楼顶上的摩天轮，被誉为“长春眼”，如图②是其正面的平面图．已知摩天活力城楼顶AD距地面BC为34米，摩天轮⊙O与楼顶AD近似相切，切点为G．测得∠OEF＝∠OFE＝67°，EF＝27.54米，求摩天轮的最高点到地面BC的距离．（结果精确到0.1米）（参考数据：sin67°＝0.92，cos67°0.39，tan67°＝2.36）

Answer 1

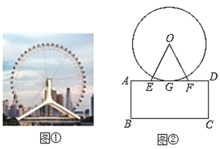
【答案】摩天轮的最高点到地面BC的距离约为99.0米．

【解析】

如图，连结OG．由切线的性质得垂直，再由等腰三角形的三线合一性质，得G为EF中点，从而在Rt△OGF中用三角函数解出OG，再乘2，加上楼顶距地面的距离即可．

解：如图，连结OG，

∵∠OEF=∠OFE，

∴OE=OF，

∵⊙O与AD相切于点G，

∴OG⊥EF，

∴∠OGF=90°，FG=EG=EF=×27.54=13.77（米），

在Rt△OGF中，∠OGF=90°，tan∠OFE=，

∴OG=FGtan∠OFG=13.77×2.36≈32.50（米），

∴32.50×2+34=99.0（米），

答：摩天轮的最高点到地面BC的距离约为99.0米．