题目内容
【题目】在同一平面直角坐标系中,一次函数y=ax+c和二次函数y=﹣ax2+c(a≠c)的图象大致为( )
A.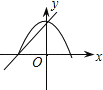 B.
B.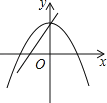
C.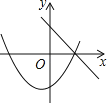 D.
D.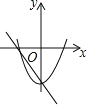
【答案】B
【解析】
可先根据一次函数的图象判断a、c的符号,求出一次函数与x轴的交点位置,再判断二次函数图象,求出二次函数与x轴的交点位置,进而判断是否相符即可.
A、由一次函数y=ax+c的图象可得:a>0,c>0,与x轴的交点坐标为(﹣![]() ,0),与y轴的交点是(0,c),此时二次函数y=﹣ax2+c的图象应该开口向下,与x轴的交点坐标为(±
,0),与y轴的交点是(0,c),此时二次函数y=﹣ax2+c的图象应该开口向下,与x轴的交点坐标为(±![]() ,0),与y轴的交点是(0,c),因为a≠c,所以两函数图象与x轴的交点不会重合,故A错误;
,0),与y轴的交点是(0,c),因为a≠c,所以两函数图象与x轴的交点不会重合,故A错误;
B、由一次函数y=ax+c的图象可得:a>0,c>0,与x轴的交点坐标为(﹣![]() ,0),与y轴的交点是(0,c),此时二次函数y=﹣ax2+c的图象应该开口向下,与x轴的交点坐标为(±
,0),与y轴的交点是(0,c),此时二次函数y=﹣ax2+c的图象应该开口向下,与x轴的交点坐标为(±![]() ,0),与y轴的交点是(0,c),因为a≠c,所以两函数图象与x轴的交点不会重合,故B正确;
,0),与y轴的交点是(0,c),因为a≠c,所以两函数图象与x轴的交点不会重合,故B正确;
C、由一次函数y=ax+c的图象可得:c>0,由二次函数y=﹣ax2+c的图象可得c<0,故错误;
D、由一次函数y=ax+c的图象可得:a<0,c<0,与x轴的交点坐标为(﹣![]() ,0),与y轴的交点是(0,c),此时二次函数y=﹣ax2+c的图象应该开口向上,与x轴的交点坐标为(±
,0),与y轴的交点是(0,c),此时二次函数y=﹣ax2+c的图象应该开口向上,与x轴的交点坐标为(±![]() ,0),与y轴的交点是(0,c),因为a≠c,所以两函数图象与x轴的交点不会重合,故D错误;
,0),与y轴的交点是(0,c),因为a≠c,所以两函数图象与x轴的交点不会重合,故D错误;
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目