Question

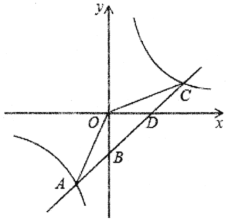
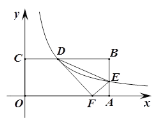
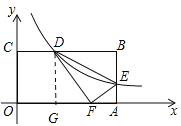
【题目】如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B 的坐标为(8,4)，反比例函数y=(k>0)的图象分别交边BC、AB 于点D、E，连结DE，△DEF与△DEB关于直线DE对称，当点F恰好落在线段OA上时，则k的值是________.

Answer 1

【答案】12

【解析】

由于四边形是矩形OABC，且△DEF与△DEB关于直线DE对称．当点F正好落在边OA上，可得△DGF∽△FAE，然后把D和E点坐标表示出来，再由三角形相似对应边成比例即可求出AF的长．然后利用勾股定理求出k=12．

过点D作DG⊥OA垂足为G（如图所示）

由题意知D（，4），E（8，），DG=4

又∵△DEF与△DEB关于直线DE对称．当点F正好落在边OA上

∴DF=DB，∠B=∠DFE=90°

∵∠DGF=∠FAE=90°，∠DFG+∠EFA=90°

又∵∠EFA+∠FEA=90°

∴∠GDF=∠EFA

∴△DGF∽△FAE

∴，即，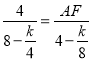

解得：AF=2，

∵EF2=EA2+AF2

即(4)2=（）2+4

解得：k=12

故答案为12