题目内容
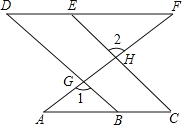
【题目】已知:如图,AC∥DF,直线AF分别直线BD、CE 相交于点G、H,∠1=∠2,求证:∠C=∠D.
解:∵∠1=∠2(已知)
∠1=∠DGH(_________________)
∴∠2=__________(______________)
∴BD∥CE(________________)
∴∠C= ________(_______________)
又∵AC∥DF
∴∠D=∠ABG(________________)
∴∠C=∠D(________________)
【答案】对顶角相等 ∠DGH 等量代换 同位角相等,两直线平行 ∠ABG 两直线平行,同位角相等 两直线平行,内错角相等 等量代换
【解析】
先由等量代换得到∠2=∠DGH,则可根据平行线的判定方法得到BD∥CE,于是根据平行线的性质得∠C=∠ABG,再由AC∥DF得到∠D=∠ABG,所以∠C=∠D.
解:∵∠1=∠2
∠1=∠DGH( 对顶角相等 ),
∴∠2=∠DGH( 等量代换 )
∴BD∥CE( 同位角相等,两直线平行 )
∴∠C=_∠ABG( 两直线平行,同位角相等 )
又∵AC∥DF
∴∠D=∠ABG(两直线平行,内错角相等)
∴∠C=∠D(等量代换).

练习册系列答案
相关题目