Question

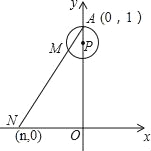
【题目】如图，在平面直角坐标系中，同时将点A（﹣1，0）、B（3，0）向上平移2个单位长度再向右平移1个单位长度，分别得到A、B的对应点C、D．连接AC，BD

（1）求点C、D的坐标，并描出A、B、C、D点，求四边形ABDC面积；

（2）在坐标轴上是否存在点P，连接PA、PC使S△PAC＝S四边形ABCD？若存在，求点P坐标；若不存在，请说明理由．

Answer 1

【答案】（1）（0，2），（4，2），见解析，ABDC面积：8；（2）存在，P的坐标为（7，0）或 （﹣9，0）或（0，18）或 （0，﹣14）．

【解析】

（1）根据向右平移横坐标加，向上平移纵坐标加写出点C、D的坐标即可，再根据平行四边形的面积公式列式计算即可得解；

（2）分点P在x轴和y轴上两种情况，依据S△PAC＝S四边形ABCD求解可得．

（1）由题意知点C坐标为（﹣1+1，0+2），即（0，2），

点D的坐标为（3+1，0+2），即（4，2），

如图所示，

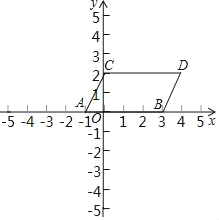
S四边形ABDC＝2×4＝8；

（2）当P在x轴上时，

∵S△PAC＝S四边形ABCD，

∴，

∵OC＝2，

∴AP＝8，

∴点P的坐标为 （7，0）或（﹣9，0）；

当P在y轴上时，

∵S△PAC＝S四边形ABCD，

∴，

∵OA＝1，

∴CP＝16，

∴点P的坐标为（0，18）或（0，﹣14）；

综上，点P的坐标为（7，0）或 （﹣9，0）或（0，18）或（0，﹣14）．