题目内容
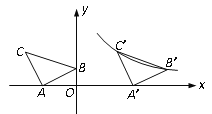
【题目】如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
(1)点C的坐标是 ;
(2)将△ABC沿x轴正方向平移得到△A′ B′C′,且B,C两点的对应点B′,C′恰好落在反比例函数![]() 的图象上,求该反比例函数的解析式.
的图象上,求该反比例函数的解析式.
【答案】(1) (-3, 2) (2)![]()
【解析】试题分析:(1)过C作CN垂直于x轴,交x轴于点N,由A、B及C的坐标得出OA,OB,CN的长,再证明Rt△CNA≌Rt△AOB,由∠CAB=90°,根据全等三角形的对应边相等可得出CN=0A,AN=0B,由AN+OA求出ON的长,再由C在第二象限,可得出点C的坐标;(2)(2)由第一问求出的C与B的横坐标之差为3,根据平移的性质得到纵坐标不变,故设出C′(m,2),则B′(m+3,1),再设出反比例函数解析式,将C′与B′的坐标代入得到关于k与m的两方程,消去k得到关于m的方程,求出方程的解得到m的值,即可确定出k的值,得到反比例函数解析式.
试题解析:
(1) (-3, 2)
(2) 解:设平移距离为a, 则点C′(-3+a,2),点B′(a,1)
∴![]() ,
, ![]() ∴2(-3+a)=a
∴2(-3+a)=a
解得a=6
∴![]() =a=6
=a=6
∴![]()

练习册系列答案
相关题目
【题目】据崇左市气象预报:我市6月份某天中午各县(区)市的气温如下:
地名 | 江州区 | 扶绥县 | 天等县 | 大新县 | 龙州县 | 宁明县 | 凭祥市 |
气温 | 37(℃) | 33(℃) | 30(℃) | 31(℃) | 33(℃) | 36(℃) | 34(℃) |
则我市各县(区)市这组气温数据的极差是 .