题目内容
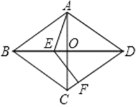
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是线段BO上的一个动点(可以与O、B重合),点F为射线DC上一点,若∠ABC=60,∠AEF=120,AB=5,则EF的取值范围是_____.
【答案】![]()
【解析】
连结CE,根据菱形的性质和全等三角形的判定可得△ABE≌△CBE,根据全等三角形的性质可得AE=CE,设∠OCE=a,∠OAE=a,∠AEO=90°-a,可得∠ECF=∠EFC,根据等角对等边可得CE=EF,从而得到AE=EF,在Rt△ABO中,根据含30°的直角三角形的性质得到AO=![]() ,可得
,可得![]() ≤AE≤5.
≤AE≤5.
如图,连结CE,
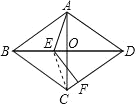
∵在菱形ABCD中,AB=BC,![]() ,BE=BE,
,BE=BE,
∴△ABE≌△CBE,
∴AE=CE,
设![]()
∴![]()
∴![]()
∵![]()
∴∠ECF=∠EFC,
∴CE=EF,
∴AE=EF,
∵AB=5,![]()
∴在Rt△ABO中,AO=![]() ,
,
∵![]()
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
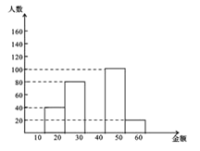
【题目】小明同学为调查某小学六个年级学生每周的零花钱情况,他在学校中随机抽取了400名学生进行调查统计并制成如下图表,
|
|
请根据图表提供的信息解答下列问题:
(1)a =__________,b =__________;
(2)补全频数分布直方图;
(3)若全校共有3000名学生,请你估计该校每周零花钱超过50元的学生有多少名?