题目内容
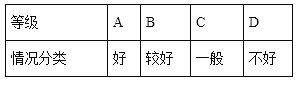
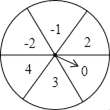
【题目】如图是一个平均被分成6等分的圆,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为x,乙转动转盘后指针所指区域内的数字为y(当指针在边界上时,重转一次,直到指向一个区域为止).
(1)直接写出甲转动转盘后所指区域内的数字为负数的概率;
(2)用树状图或列表法,求出点(x,y)落在第二象限内的概率.
【答案】(1)甲转动转盘后所指区域内的数字为负数的概率为![]() ;
;
(2)点(x,y)落在第二象限内的概率为![]() .
.
【解析】试题分析:(1)根据古典概率的知识,利用概率公式即可求得答案;
(2)根据题意列出表格,然后根据表格即可求得所有等可能的结果与点(x,y)落在第二象限内的情况,然后利用概率公式求解即可求得答案.
解:(1)∵一共有6种等可能的结果,甲转动转盘后所指区域内的数字为负数的有:﹣1,﹣2共2种情况,
∴甲转动转盘后所指区域内的数字为负数的概率为:![]() =
=![]() ;
;
(2)根据题意,列表得:
甲 乙 | ﹣1 | ﹣2 | 0 | 2 | 3 | 4 |
﹣1 | (﹣1,﹣1) | (﹣2,﹣1) | (0,﹣1) | (2,﹣1) | (3,﹣1) | (4,﹣1) |
﹣2 | (﹣1,﹣2) | (﹣2,﹣2) | (0,﹣2) | (2,﹣2) | (3,﹣2) | (4,﹣2) |
0 | (﹣1,0) | (﹣2,0) | (0,0) | (2,0) | (3,0) | (4,0) |
2 | (﹣1,2) | (﹣2,2) | (0,2) | (2,2) | (3,2) | (4,2) |
3 | (﹣1,3) | (﹣2,3) | (0,3) | (2,3) | (3,3) | (4,3) |
4 | (﹣1,4) | (﹣2,4) | (0,4) | (2,4) | (3,4) | (4,4) |
∴点(x,y)的坐标一共有36种等可能的结果,且每种结果发生的可能性相等,其中点(x,y)落在第二象限的结果共有6种,
∴点(x,y)落在第二象限内的概率为:![]() =
=![]() .
.

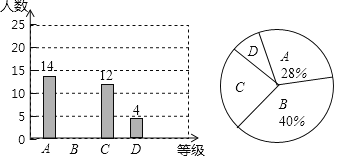
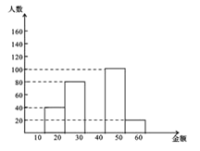
【题目】小明同学为调查某小学六个年级学生每周的零花钱情况,他在学校中随机抽取了400名学生进行调查统计并制成如下图表,
|
|
请根据图表提供的信息解答下列问题:
(1)a =__________,b =__________;
(2)补全频数分布直方图;
(3)若全校共有3000名学生,请你估计该校每周零花钱超过50元的学生有多少名?