题目内容
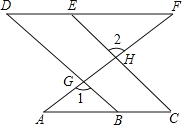
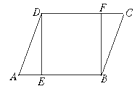
【题目】如图,在平行四边ABCD中,E、F分别是AB、DC上的点,且AE=CF,
(1)求证:△ADE≌△CBF;
(2) 当∠DEB=90°时,试说明四边形DEBF为矩形.
【答案】(1)证明见解析(2)四边形DEBF是矩形.
【解析】试题分析:(1)利用平行四边形的性质,根据SAS即可证明.
(2)首先证明四边形DEBF是矩形,由∠DEB=90°,即可推出四边形DEBF是矩形.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,
在△ADE和△CBF中,
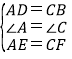
∴△ADE≌△CBF(SAS).
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AE=CF,
∴BE=DF,
∴四边形DEBF是平行四边形,
∵∠DEB=90°,
∴四边形DEBF是矩形.

练习册系列答案
相关题目
【题目】某商场计划用3300元购进甲,乙两种商品共100个,这两种商品的进价、售价如下表:
进价(元/个) | 售价(元/个) | |
甲种 | 25 | 30 |
乙种 | 45 | 60 |
(1)求甲、乙两种商品各进多少个?
(2)全部售完100个商品后,该商场获利多少元?