Question

【题目】如图，在ABCD中，点E，F是直线BD上的两点，DE=BF．

（1）求证：四边形AFCE是平行四边形．

（2）若BD⊥AD，AB=5，AD=3，四边形AFCE是矩形，求DE的长．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）首先根据题干所给信息可以求出，进一步可以证明四边形AFCE是平行四边形.

（2）根据题干可求出BD的长度，再连接AC进而求出AO的长度，最后推出DE的长度.

（1）证明：∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC

∴∠ADB=∠CBD，

∴∠ADE=∠CBF，

又∵DE=BF，

∴（SAS），

∴AE=CF，∠AED=∠CBF，

∴AE∥CF，

∴四边形AFCE是平行四边形.

（2）∵，AB=5，AD=3，

∴ ，

连接AC交EF于O，

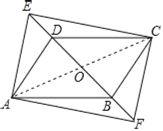
∴DO=BD=2，

∴AO=，

∵四边形AFCE是矩形，

∴AC=EF，AO=AC，EO=EF，

∴AO=EO=，

∴DE=EODO=.